Лінійна регресія

Припустимо, що форма функціональної залежності між змінними x та y, відома з точністю до параметрів a 0, a 1, ..., ak–1 і має вигляд

y = f (x, a0, a1, ..., ak–1). (9.101)

Функція f називається функцією регресії величини Y на X, а співвідношення (3.101) – рівнянням регресії Y на X. Вимагається за результатами спостережень (вибірки) (xi, yi) , i = 1, 2, ..., знайти оцінки невідомих параметрів a 0, a 1, ... , a k–1.

Завданнями регресійного аналізу є:

1) встановлення форми залежності. Як правило, ця форма стає відомою за даними спостережень (див. Рис. 3.15), де точки (xi ; y i) – значення вибірок (вимірювань)

а б в

Рис. 9.15

2) визначення функції регресії (9.100). Процес знаходження функції регресії називається вирівнюванням окремих значень залежної змінної;

3) оцінка невідомих значень залежної змінної y за оцінками параметрів, що входять в рівняння регресії.

Розглянемо частковий випадок функцій регресії – лінійні функції y = a + bx, які називаються регресійними прямими, або прямими регресії.

Нехай (xi, yi) – спостережувані (точні) значення, а – наближені значення yi, обчислені із рівняння регресії. Тоді величина є відхиленням наближеного значення від точного yi(див. Рис. 9.16).

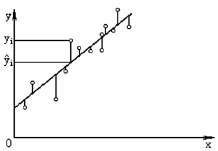
Рис. 9.16

За методом найменших квадратів невідомі параметри a і b прямої регресії знаходяться із умов мінімізації суми квадратів відхилень, тобто із умов мінімізації функції

.

Прирівнявши частинні похідні Sa¢ та Sb¢ до нуля, отримаємо систему нормальних рівнянь

Розв’язавши її, знайдемо

(9.102)

Легко показати, що для значень a та b, обчислених за формулами (3.102), функція S(a, b) набуває мінімуму.

Якщо необхідно за експериментальними даними отримати лінійне рівняння регре-сії X та Y, то в рівнянні регресії y = a + bx потрібно поміняти місцями змінні x та y. При цьому одержимо рівняння x = a¢ + b ¢y, де a¢ та b ¢ обчислюються за формулами

(9.103)

Відзначимо, що регресійні прямі y = a + bx та x = a¢ + b ¢y є різними. Перша пряма отримується в результаті розв’язання задачі про мінімізацію суми квадратів відхилень по вертикалі, а друга – при розв’язанні задачі про мінімізацію суми квадратів відхилень по горизонталі.

На практиці для знаходження рівнянь регресії складається таблиця 9.15.

Таблиця 9.15

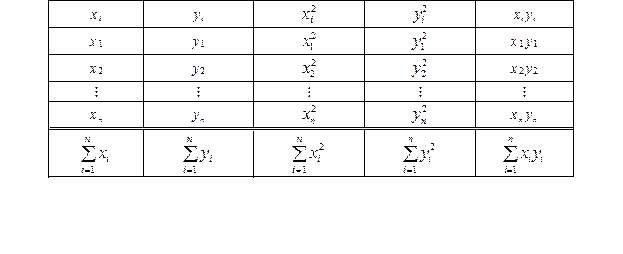
В даній таблиці в останньому рядку суми i визначають коефіціенти a та b або a¢ та b¢ за формулами (3.102) або (3.103) відповідно.

Рівняння лінійної регресії можна побудувати, використовуючи вибірковий коефіцієнт кореляції

– рівняння прямої регресії Y на X,

– рівняння прямої регресії X на Y,

де – середні вибіркові; rx/y, ry/x– коефіціенти лінійної регресії; S0x, S0y– виправлені середні квадратичні відхилення вибірок;

; .

Прямі регресії проходять через точку . Вони збігаються, якщо .

Вибірковий коефіцієнт кореляції є середнім геометричним коефіцієнтів лінійної регресії.

Приклад 19.За даними таблиці спостережень

скласти рівняння регресії Y на X та X на Y.

Складемо таблицю 9.16.

Таблиця 9.16

За формулами (3.102) для n = 3 отримуємо

Отже, рівняння регресії Y на X буде

Аналогічно за формулами (3.103) знаходимо:

Рис.9.17

Звідси рівняння X на Y буде

Із отриманих рівнянь видно, що регресійні прямі та є дійсно різними. Побудуємо їх (див. Рис.9.17).