
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Однофакторний комплекс
Нехай деякий геодезичний об’єкт (кут, довжина лінії, перевищення і т.д.)
декілька спостерігачів вимірюють однаковими інструментами, певною кількістю прийомів в один і той же час.
Досліджується однорідність результатів спостережень відносно центра групування. Тобто, якщо присутні систематичні похибки, то вони одного порядку. При цьому точність спостережень вважаєтьсяоднаковою (тобто характери-зується однаковим параметром s). Цим самим ми хочемо перевірити вплив одного фактора (спостерігача) на результати спостережень.
Результати вимірювань якоїсь фізичної величини m спостерігачами n разів кожним можна подати у вигляді таблиці 3.8.
Таблиця 7.8
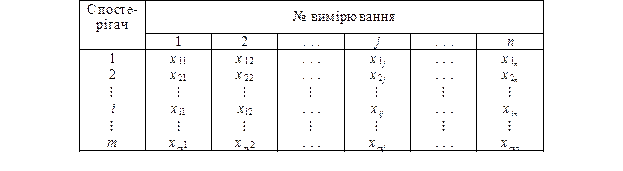
Кожний рядок цієї таблиці євибіркою. Таких вибірок буде m.
Знайдемо середнє арифметичне значення із цих вибірок
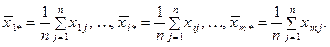
Якщо систематичні похибки, які викликані різною кваліфікацією спостерігачів, не однакові, то можна очікувати підвищеного розсіювання вибіркових середніх.
Отже, в статистичному сенсі задача полягає в перевірці гіпотези H0:

та порівнянні з альтернативною гіпотезою H1:
 ,
,
де – математичні сподівання генеральних сукупностей, із яких взято вибірки.
Інакше кажучи, якщо виконується гіпотеза H0, то систематичних впливів немає взагалі, а якщо H1– систематичні впливи значні.
Але може бути і така ситуація, коли систематичні впливи є і ними можна нехтувати.
Статистична гіпотеза H0перевіряється порівнянням групових (в рядках) та міжгрупових (в стовпчиках) вибіркових дисперсій за F-критерієм (критерієм Фішера). Якщо цей критерій показує незначне розходження між груповою та
міжгруповою вибірковими дисперсіями, то гіпотеза H0приймається і можна зробити висновок, що результати спостережень не мають систематичних впливів.
Для знаходження відповідних вибіркових дисперсій знайдемо суму квадратів відхилень
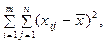 (7.81)
(7.81)
де – загальне середнє.
Перетворимо вираз (3.81)

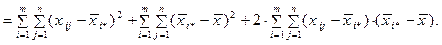 (7.82)
(7.82)
Із отриманого виразу (3.82) випишемо третю суму
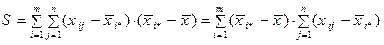 .
.
Але , оскільки є сумою відхилень спостережень i-ої серії від середнього тої ж самої серії і тому
S = 0.
Друга сума зі співвідношення (3.82) буде
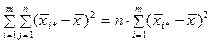 .
.
Тоді вираз (3.82) перепишемо так:
 , (7.83)
, (7.83)
або
Q = Q1+ Q2,
дедоданок Q1 – це сума квадратів різниць між середніми окремих сукупностей (груп, рядків в нашому прикладі) та загальним середнім всієї сукупності. Вонаносить назвусума квадратів відхилень “між групами” та характеризує систематичні розходження між сукупностями спостережень. Це є“розсіювання за факторами”;
доданок Q2 – це сума квадратів різниць між окремими спостереженнями та середнім відповідної сукупності. Вона називаєтьсясумою квадратів відхилень “в середині груп” і характеризує залишкове розсіювання випадкових похибок результатів вимірювань;
Q –загальна або“повна” сума квадратів відхилень окремих спостережень від загального середнього .
Припустимо тепер, що гіпотеза H0: рівність центрів (а значить однаковість систематичних похибок) є вірною. Тоді нормальні розподіли всіх похибок є тотожними, тобто мають однаковий центр і дисперсію s2. Тому всі m×n спостережень можна розглядати як вибірку із однієї і тієї ж генеральної сукупності, а величину вважати як незміщену оцінку дисперсії s2, знайдену за цією вибіркою. Величина , а значить і , мають c2– розподіл із (mn – 1), (m – 1), m(n – 1) ступенями довільності відповідно.
При цьому розподіл цих величин справедливий для будь-яких припущень відносно центрів розподілу.
Припустивши, що нульова гіпотеза H0є справедливою, суми квадратів Q, Q1, Q2можна використати для отримання незміщених оцінок для дисперсії s2генеральної сукупності
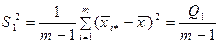 – оцінка дисперсії за фактором, (7.84)
– оцінка дисперсії за фактором, (7.84)
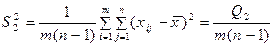 – оцінка залишкової дисперсії, (7.85)
– оцінка залишкової дисперсії, (7.85)
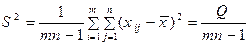 – оцінка загальної дисперсії. (7.86)
– оцінка загальної дисперсії. (7.86)
Оцінка різниці між дисперсіями отримується за критерієм Фішера
 .
.
Далі, за обраним рівнем значущості a і таблицею F-розподілу (див. Додаток, табл. 5) знаходять межу критичної області Fa, маючи на увазі, що P(F > Fa) = a.
Якщо F £ Fa, то можна стверджувати, що нульова гіпотеза H0приймається, тобто вплив різних виконавців спостережень (у нашому прикладі) не має суттєвих систематичних похибок, а оцінки дисперсій відмінні між собою тільки за рахунок випадкових факторів.
Однофакторний дисперсійний аналіз можна зобразити таблицею 7.9.
Таблиця 7.9
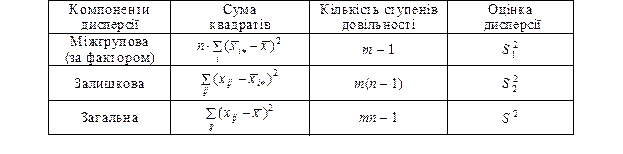
Дата добавления: 2014-12-03; просмотров: 458; Мы поможем в написании вашей работы!; Нарушение авторских прав |