Другий випадок.

Нульова гіпотеза є Н0: D(X) = D(Y) а конкуруюча – Н1: D(X) ¹ D(Y). У такому випадку будують двобічну критичну область (див. Рис. 3.12).

Для отримання найбільшої потужності критерія потрібно, щоб виконувались співвідношення

. (6.68)

Через те, що таблиця критичних точок розподілу Фішера–Снедекора не має лівих критичних

за заданим рівнем значущості і ступенями довільності k1і k2. Що стосується лівої критичної точки F1, то за методом введення спеціальної функції ймовірність події замінюють ймовірністю

.

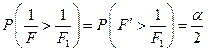Таким чином, ліва критична точка F – розподілу замінюється на праву критичну точку F ¢ – розподілу зі ступенями довільності k1, k2 тобто достатньо шукати тільки праву критичну точку

,

де числа k1, k2– кількість ступенів довільності більшої та меншої дисперсії відповідно.

Якщо Fобч.< Fq, то немає підстав відхиляти нульову гіпотезу, а якщо Fобч.> Fq, то нульова гіпотеза H0– відхиляється.

Приклад 10. Перевіримо тепер, чи можна вважати несуттєвими відхилення вибіркових дисперсій ; .

Розв’язання.

1). Сформулюємо гіпотези Н0: D(X) = D(Y), Н1: D(X) ¹ D(Y).

2). Знайдемо числове значення критерія перевірки

.

3). За рівнем значущості a = 0,02, k1= 5 –1 = 4 і k2= 6 – 1 = 5 знаходимо праву критичну точку двобічної критичної області

.

4). Оскільки Fобч.< Fq пр., то гіпотеза Н0приймається. Це означає, що різницю між вибірковими дисперсіями можна пояснити випадковими причинами.

6.6. Перевірка гіпотези про рівність дисперсії нормально розподіленої генеральної сукупності деякому гіпотетичному значенню

Розглянемо нормально розподілену генеральну сукупність із невідомою дисперсією. При цьому є підстави припустити, що вона дорівнює деякому (гіпотетичному) значенню .

Отже, перевіряємо таку нульову гіпотезу .

На практиці така гіпотеза виникає тоді, коли потрібно перевірити точність приладів, інструментів, методів досліджень та стійкість технологій.

Критерієм перевірки є

(6.69)

якщо невідоме математичне сподівання генеральної сукупності і

, (6.70)

якщо mx– відоме.

Дана статистика має c2- розподіл з k = n – 1 ступенями довільності у випадку (3.69) і k = n ступенями довільності у випадку (3.70). Критична область, як відомо, будується в залежності від конкуруючої гіпотези.