Порівняння вибіркового середнього з гіпотетичним генеральним середнім нормально розподіленої сукупності

Така задача виникає тоді, коли є відомим наперед значення середнього арифметичного (його називають гіпотетичним).

Наприклад, якщо деяка генеральна сукупність X{x1, x2, ..., xn} – є сукупністю розмірів xiвертикального круга оптичного теодоліта, який виготовляється станком – автоматом. Тоді можна припустити, що генеральне середнє значення a цих розмірів дорівнює проектному розміру a0. Щоб перевірити таке припущення знаходять вибіркове середнє і встановлюють чи є суттєвими розбіжності
між та a0.

Якщо виявиться, що розбіжності є несуттєвими, тоді станок забезпечує в середньому проектний розмір; якщо розбіжності є суттєві, тоді станок треба налагодити.

При таких дослідженнях можуть виникати ситуації, коли генеральну дисперсію можна вважати відомою і можуть траплятися випадки, коли вона є невідома.

Припустимо, що генеральна дисперсія – відома або з попередніх досліджень, або знайдена теоретично, або за вибіркою дуже великого обсягу.

Нехай, за вибіркою обсягом n знайдено середнє , а відому генеральну дисперсію позначимо через s2.

Зауважимо, що вибіркове середнє є незміщеною, ефективною і слушною оцінкою генерального середнього a, тобто . Тоді і за нульову гіпотезу можна прийняти H0: або H0: a = a0.

За критерій перевірки беремо нормоване відхилення вигляду

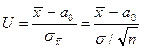(6.62)

яке розподілено нормально з параметрами M[U] = 0, s2[U] = 1, якщо гіпотеза H0є справедливою.

Критична область, як і при перевірці попередніх гіпотез, будується в залежності від вигляду альтернативної гіпотези.

1. Якщо альтернативною гіпотезою є гіпотеза H1: a ¹ a0, то знаходиться критична точка двобічної критичної області за допомогою таблиці для функції Лапласа і з використанням рівності

,

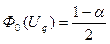де – вибраний рівень значущості.

Далі обчислений критерій

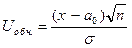
порівнюється з критичним значенням Uq.

Якщо |Uобч.| < Uq, то немає підстав відхилити гіпотезу H0, а якщо |Uобч.| > Uq, то H0відхиляється.

2. При альтернативній гіпотезі H1: a > a0критична область буде правобічною і критична точка знаходиться з виразу

.

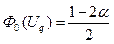Якщо Uобч.< Uq, то нульова гіпотеза Н0приймається для досліджуваної вибірки, а якщо Uобч.> Uq, то гіпотеза Н0відхиляється.

3. При конкуруючій гіпотезі H1: a < a0критична область лівобічна. Критичну точку знаходять так, як і у пункті 2, а потім приймають до уваги, що

.

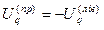Якщо Uобч.> Uq, то підстав відхилити гіпотезу Н0немає, а якщо Uобч.< –Uq, то гіпотеза Н0відхиляється.

Приклад 8.Із нормально розподіленої сукупності з відомим середнімквадратичним відхиленням s = 0,36 сформовано вибірку обсягом n = 36, за якою знайдено середнє вибіркове . За рівнем значущості потрібно перевірити гіпотезу H0: a = a0= 21.

Розв’язання.

1). H0: a = a0= 21. Нехай альтернативною гіпотезою буде гіпотеза H1: a > 21.

2). Обчислюємо вибіркове значення критерію за формулою (3.62)

.

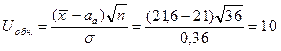3). .

4). За умовою альтернативної гіпотези критична область буде правобічною і критичну точку будемо шукати за таблицею для функції Лапласа з допомогою виразу

,

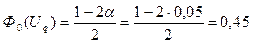Uq= 1,65.

5). Оскільки Uобч.> Uq(10 > 1,65), то гіпотеза Н0відхиляється, а це означає, що розбіжність між вибірковим середнім і гіпотетичним середнім є суттєвою.

Розглянемо випадок, коли дисперсія генеральної сукупності є невідомою. Така ситуація виникає у випадку малих вибірок. За критерій перевірки гіпотези приймають випадкову величину

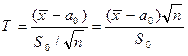(6.63)

де S0– виправлене середнє квадратичне відхилення (незміщена оцінка). Ця величина має розподіл „Studenta” з k = n – 1 ступенями довільності. Критична область за обраним рівнем значущості будується також в залежності від альтернативної гіпотези.

1. При H0: a = a0, H1: a ¹ a0для обчисленого значення критерія

за таблицею критичних точок розподілу „Studenta” (див. Додаток, табл.4) шукають критичну точку двобічної критичної області tq двобіч.(a, k).

Якщо |Tобч.| < tq двобіч., то гіпотеза Н0приймається, а якщо |Tобч.| > tq двобіч.(a, k), то вона відхиляється.

2. Якщо конкуруючою гіпотезою є H1: a = a0, то зa тими самими таблицями знаходимо межу (критичну точку) правобічної критичної області tq правобіч.(a, k). Тоді, якщо Tобч.< tq правобіч.(a, k), немає підстав відхиляти гіпотезу Н0, а якщо
Tобч.> tq правобіч.(a, k), то гіпотеза Н0відхиляється.

3. Якщо конкуруючою гіпотезою є Н1: а < а0, то критична область є лівобічною. Але шукають критичну точку таку ж, як і в пункті 2 tq правобіч.(a, k), а потім приймають до уваги, що tq лівобіч.(a, k) = –tq правобіч.(a, k). Тоді, якщо Tобч.> –tq правобіч.(a, k), то нульову гіпотезу Н0приймають, в протилежному випадку її відхиляють.

Приклад 9. За вибіркою обсягом n = 20 знайдено вибіркове середнє і виправлене середнє квадратичне відхилення s0= 4,5. Потрібно за рівнем значущості a = 0,05 перевірити гіпотезу Н0: а = а0= 15 при альтернативі Н0: а ¹ 15.

Розв’язання.

2). Обчислюємо вибіркове значення критерію за формулою (3.63)

3).

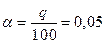
4). За умовою альтернативної гіпотези критична область тут є двобічною. Тому за таблицею критичних точок розподілу „Studenta” (див. Додаток, табл. 4), рівнем значущості a = 0,05 і числом k = n – 1 = 19 знаходимо критичну точку
tq двобіч.(0,05; 19) = 2,09.

5). Оскільки |Tобч.| < tq двобіч.(0,99 < 2,09), то гіпотеза Н0приймається, а це означає, що різниця між вибірковим середнім та гіпотетичним значенням a0є незначною і пояснюється випадковими причинами.