Перший випадок.

Нульова гіпотеза H0: M(X) = M(Y) , а альтернатива H1: M(X) ¹ M(Y). У такому випадку будують двобічну критичну область, таку, щоб ймовірність потрапляння в неї дорівнювала прийнятому рівневі значущості (якщо H0– справедлива). Найбільша потужність критерія (ймовірність потрапляння у критичну область, якщо справедлива гіпотеза H1) буде тоді, коли “ліва” та “права” критичні точки вибрані так, щоб ймовірність потрапляння критерія у кожний з двох інтервалів критичної області дорівнювала (див. Рис. 3.9)

(3.46)

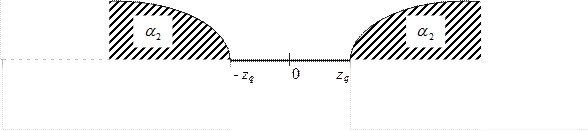
Рис. 6.9

Ці точки, як бачимо, симетричні відносно нуля. Отже, можна знаходити тільки праву межу, щоб отримати двобічну критичну область

.

Областю прийняття гіпотези H0буде інтервал

.

Критичну точку zqшукаємо за допомогою функції Лапласа Ф0(z), знаходячи ймовірність потрапляння нормованої нормально розподіленої випадкової величини Z на інтервал (0, z) . (3.47)

Оскільки розподіл Z симетричний відносно нуля, то можна записати

. (6.48)

Розбивши промінь (0; ¥) на інтервал (0; zq) та інший промінь (zq; ¥), маємо

. (6.49)

Із виразів (3.46), (3.47) та (3.49) отримаємо

,

звідки

. (6.50)

Отже, користуючись виразом (3.50), за вибраним рівнем значущості a, та таблицею для функції Лапласа знаходимо zq. Обчислене за виразом (3.45) значення критерія позначимо zобч.або zспост.– спостережуване значення критерія.

Якщо |zобч.| < zq, то немає підстав відхилити гіпотезу H0; якщо |zобч.| > zq, то гіпотезу H0відхиляють, тобто вибіркові середні досліджуваних генеральних сукупностей суттєво відрізняються між собою.