Довірчий інтервал для оцінки дисперсії і середнього квадратичного відхилення

Розглянемо нормально розподілену величину X. Потрібно побудувати довірчий інтервал для невідомої дисперсії генеральної сукупності за вибірковими її оцінками S2або . Відомо, що обидві оцінки мають c2– розподіл з k = n – 1 ступенями довільності.

Запишемо вираз для S2

,

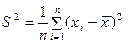введемо позначення і утворимо рівність

,

яку поділимо на

.

Права та ліва частини в отриманій рівності мають c2– розподіл з k = n – 1 ступенями довільності, оскільки – стале число, а чисельники є сумами квадратів певних величин.

Побудуємо довірчий інтервал для дисперсії із використанням величини . Для цього з обраною довірчою ймовірністю g = 1 – a запишемо

. (5.38)

На графіку c2– розподілу (див. Рис. 3.7) це можна зобразити так:

Рис. 3.7

Тобто величина займає певну площу під кривою густини c2– розподілу, обмежену двома ординатами в точках і . При цьому слід пам’ятати, що точки можуть змінювати своє положення, а площа буде сталою (вона задається ймовірністю g = 1 – a).

Величини і вибирають так, щоб виконувалась умова

, (5.39)

тобто ймовірність виходу величини, яка має c2– розподіл, за межі відрізка є однаковою як ліворуч, так і праворуч, і дорівнює (a визначає q%-ну критичну точку розподілу статистики c2). Далі з врахуванням рівності (3.39) запишемо

. (5.40)

Оскільки площа під кривою c2– розподілу фіксується ліворуч ймовірністю , то її можна розглядати як ймовірність протилежної події в порівнянні з ймовірністю , тобто

.

Інакше кажучи, q %-ні критичні точки c2– розподілу визначатимутьсяймовірностями ліворуч і праворуч.

Тепер, перетворимо нерівність

так, щоб можна було оцінювати .

Розглянемо, дві еквівалентні нерівності

та ,

які запишемо у вигляді

та

та об’єднаємо в одну нерівність

.

Тоді

. (5.41)

Отже буде довірчим інтервалом для невідомої дисперсії .

Для середнього квадратичного відхилення матимемо

(5.42)

– довірчий інтервал для середнього квадратичного відхилення.

Приклад 4. Побудувати довірчий інтервал з надійністю g = 0,96 для невідомої дисперсії генеральної сукупності спостережень випадкової величини X, розподіленої нормально, за вибіркою із обсягом n = 20 та відомою виправленою вибірковою дисперсією .

Розв’язання.

1. За довірчою ймовірністю g = 0,96 обчислимо такі величини:

g = 1 – a = 0,96, a = 0,04, a /2 = 0,02.

Це означає, що , а .

2. Обчислимо кількість ступенів довільності для величини

k = n – 1 = 19.

3. За таблицею критичних точок c2– розподілу, ймовірностями , і числом k =19 знаходимо , .

4. Будуємо довірчий інтервал, використовуючи рівність (3.41)

,

або

.

Остаточно отримаємо

.

Якщо потрібно побудувати довірчий інтервал для середнього квадратичного відхилення, то використовуємо рівність (3.42) і остаточно одержимо

.