Лекція 4. Точні розподіли деяких вибіркових характеристик

Даний розподіл має випадкова величина, яка є сумою квадратів незалежних випадкових величин, які підпорядковуються нормальному закону розподілу з математичними сподіваннями та дисперсіями

.

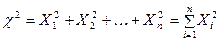c2– розподіл (хі – квадрат розподіл) задається функцією густини ймовірностей

(4.23)

де – гама-функція, k – число, пов’язане з обсягом вибірки n і називається “кількістю ступенів довільності”. Число k визначається як різниця між кількістю випадкових величин (обсягом вибірки n) і кількістю зв’язків між ними (лінійних співвідношень).

Наприклад, завжди існує таке співвідношення між випадковими величинами, які утворюють вибірку:

,

оскільки середнє арифметичне є оцінкою центра розподілу mx. Тому для c2– розподілу k = n – 1.

Із виразу (4.23) видно, що густина c2– розподілу залежить тільки від одного параметра n (або k). Графік функції fk(x) для різних значень k показано на рис.3.5.

Із рисунка видно, що c2– розподіл розташовано праворуч від початку координат і зі збільшенням k він наближається до нормального розподілу. Функція fk(x), а також інтеграл ймовірностей

(4.24)

де – вибіркове середнє квадратичне відхилення. Закон розподілу t – статистики знайдено В.Госсетом (псевдонім „Student”) у вигляді функції густини розподілу

. (4.27)

Графік функції густини ймовірностей sk(x) симетричний відносно осі ординат (див.Рис.4.6), а це значить, що M[t] = 0. Дисперсія розподілу „Studenta” дорівнює . Із зростанням k крива t – розподілу наближається до кривої нормального розподілу f(x; 0; 1), а для значень k > 30 розподіл t можна замінити нормальним розподілом.

Рис. 4.6

Функція розподілу (інтегральний закон) має вигляд

. (4.28)

Диференціальна та інтегральна функції t – розподілу є протабульованими для різних k і значення їх поміщено у відповідні таблиці. Також побудовано таблиці критичних точок t – розподілу (див. Додаток, табл.4)

, (4.29)

що визначають частину площі в % під кривою густини розподілу “studenta”, яку займає статистика t.

Важливе застосування в дисперсійному аналізі має статистика F

, (4.30)

де незалежні випадкові величини U і V розподілені за законом c2з k1і k2ступенями довільності відповідно. Диференціальна функція розподілу, графік якої зображено рисунком 4.7 (густина ймовірностей випадкової величини F) має вигляд

(4.31)

а відповідна їй функція розподілу називається F – розподілом (або розподілом Фішера-Снедекора) із k1та k2 ступенями довільності, які є параметрами розподілу.

Таблиці (див. Додаток, табл.5) для F – розподілу використовуються такі, де за відомими k1і k2 можна знайти значення Fq, для якого

, (4.32)

тобто Fq– це q – відсоткова верхня межа розподілу F.

Як правило, використовують значення q = 5%, q = 2,5%, q = 1% зі широким діапазоном величин k1і k2.

Розглянемо тепер практичне застосування наведених теоретичних розподілів у різних задачах математичної статистики.