Статистичні (варіаційні) ряди та їх характеристики

1. Бойчик І.М., Харів П.С., Хопчан М.І. Економіка підприємств. - Львів: В-во "Сполом".-1998. - 212 с.

2. Бойчик І.М. Економіка підприємства: Навчальний посібник .-К.: Атіка,2004. - 480 с.

3. Харів П.С., Собко О.С., Вашків О.П. Збірник задач і тестів з економіки, організації і планування діяльності промислового підприємства. / За ред. П.С.Харіва .- Тернопіль: Підручники і посібники, 2003. - 256 с

4. Мелешко В.К. Экономика, организация и планирование в торфяном производстве: Сб.задач - Мн.:Вышэйшая школа. 1986. - 99 с.

5. Економіка підприємства: Навч. посіб./ За ред. А.В.Шегди.-К.: Знання, 2005. - 431с.

6. П.В.Круш, В.І.Подвігіна, Б.М.Сердюк та ін.

Економіка підприємства: Навчальний посібник /за заг. ред. П.В.Круша, В.І.Подвігіної, Б.М.Сердюка. – К.:Ельга-Н,КНТ, 2007. – 780с.

7. Економіка підприємства. Підручник - В 2т. / За ред. С.Ф.Покропивного. - К.: "Хвиля- Прес". 1995.

Конспект лекцій

Емпіричні методи програмної інженерії

Лекція 1.

статистичні (варіаційні) ряди та їх характеристики

Збір експериментальних даних називають статистичним спосте-реженням. Його метою є реєстрація об’єктів спостереження, які складають деяке масове явище. Отриманий зі статистичного спостереження первинний матеріал для подальшого використання та виявлення типових рис явища, яке вивчається, треба певним чином згрупувати. Для цього спостережені об’єкти слід розподілити в групах так, щоб кожна з цих груп складалася з якісно (а часто і кількісно) однорідних в певному відношенні елементів.

Наприклад, маємо партію деталей (нехай це буде лімб теодоліта). Якісною ознакою може бути його (лімба) стандартність, а кількісною – розмір (діаметр).

Інколи виконують суцільне дослідження, тобто досліджують кожний із об’єктів сукупності відносно ознаки, яка цікавить дослідника. Однак, таке дослідження на практиці буває не частим (особливо, якщо сукупність містить в собі велику кількість об’єктів). Найчастіше вибирають зі всієї сукупності обмежену кількість об’єктів та вивчають їх.

Таку випадково відібрану сукупність об’єктів називають вибірковою сукупністю або вибіркою. Сукупність всіх об’єктів, із яких проведено відбір, називають генеральною сукупністю.

Кількість об’єктів генеральної або вибіркової сукупності називають обсягом. Наприклад, з N = 1000 лімбів відібрати n = 100 для дослідження його діаметра. Тут N = 1000 – обсяг генеральної сукупності, а n = 100 – обсяг вибірки. Різниця між найбільшим і найменшим елементами вибірки називається її розмахом.

Вибірки можуть бути повторними та безповторними. Безповторна – це така вибірка, коли відібраний об’єкт у генеральну сукупність не повертається, а повторна – це вибірка, коли відібраний об’єкт повертається у генеральну сукупність перед вибором наступного. На практиці в більшості випадків користуються безповторним випадковим відбором.

Для того, щоб за даними вибірки впевнено судити про ознаку, яка цікавить дослідника, необхідно, щоб об’єкти вибірки правильно її (ознаку) зображали. Дану вимогу коротко формулюють так: вибірка повинна бути репре-зентативною (представницькою). Така ситуація буде при умові, коли кожний об’єкт має однакову ймовірність попасти у вибірку.

Існують також різні методи відбору. Їх можна поділити на два види.

Перший – відбір, який не вимагає поділу генеральної сукупності на частини; сюди відносяться:

а) простий, випадковий безповторний відбір;

б) простий, випадковий повторний.

Другий – відбір, при якому генеральну сукупність поділяють на частини; сюди відносяться:

а) типовий відбір;

б) механічний;

в) серійний.

Типовим називають відбір, при якому об’єкти відбираються не зі всієї генеральної сукупності, а з кожної її типової частини. Наприклад, якщо деталі (у нашому прикладі лімби) виготовлено на різних станках, то відбір роблять тільки з тих деталей, які виконано на одному станку.

Такий відбір роблять тоді, коли ознака, яка досліджується, коливається у різних типових частинах генеральної сукупності.

Механічним – називають відбір, при якому генеральна сукупність механічно поділяється на стільки груп, скільки об’єктів повинно увійти до вибірки, і з кожної такої групи відбирається один об’єкт. Наприклад, якщо треба відібрати 20 % виготовлених лімбів, то відбирають кожний п’ятий лімб, а якщо 5% – тоді кожний двадцятий лімб.

Слід зауважити, що можуть бути випадки, коли механічний відбір може не забезпечити репрезентативності вибірки.

Серійний відбір – це такий, коли об’єкти відбирають із генеральної сукупності не по одному, а цілими серіями, які досліджуються суцільно. Наприклад, зі станків-автоматів (якщо їх багато) вибирають групу виробів із деяких з них. частіше відбір буває комбінованим, коли розбивають генеральну сукупність випадковим чином на серії однакового обсягу, а потім простим випадковим відбором з кожної серії беруть окремі об’єкти.

Отже, вибірки є тим первинним статистичним матеріалом, який використовується для подальших досліджень. Для зручності елементи вибірок оформляють у вигляді таблиць, які називають статистичними рядами.

Простим статистичним рядом називається таблиця, в якій у першому рядку записують номер (і) експерименту (елемента вибірки), а у другому рядку відповідне спостережене значення випадкової величини хі, яке називається варіантою. Таблиці такого вигляду називають ще статистичними рядами незгрупованих даних.

Як правило, буває так, що спостережені значення хі (і = 1, 2, …, n) зустрічаються не один раз. Тоді обчислюють кількість разів mi(частоту), з якою зустрічається кожне спостережене значення, і будують ряд за зростаючим порядком варіант у першому рядку, а у другому записують відповідні частоти mi. Такий ряд називається варіаційним.

Інколи варіаційні ряди будують за відносними частотами

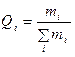, (1.1)

де 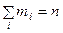– обсяг вибірки.

Нехай, наприклад, вивчається ознака – діаметр лімба. Відібрано 50 лімбів з розміром діаметра в мм: 83, 82, 84, …, 79, 81, 85, 82, 81; n = 50 – обсяг вибіркової сукупності. Позначимо ознаку, що вивчається, через X , тоді кожне спостережене значення цієї ознаки (варіанти) буде x1, x2, ..., xn(тобто 83, 85, …), а числа m1, m2, ..., mnїх частотами.

Розмістивши окремі значення ознаки у зростаючому порядку та вказавши поряд частоту ознаки, отримаємо розподіл ознаки у вигляді варіаційного ряду (див. табл. 1.1)

Таблиця 1.1

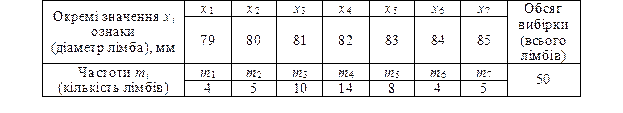
Такий ряд характеризує зміну (варіацію) деякої кількісної ознаки (в нашому випадку діаметра лімба).

Варіація ознаки може бути дискретною і неперервною.

Дискретною варіацією називається така, коли окремі значення ознаки (варіанти) відрізняються між собою на деяку скінчену величину (як правило, на ціле число).

Неперервною називається варіація, при якій значення ознаки відрізняються між собою на як завгодно малу величину. Наприклад, похибка у числовому значенні діаметра лімба (або в довжині його кола). При неперервній варіації (іноді при дискретному такті) розподіл ознаки зображають так званим інтервальним статистичним рядом. У цьому випадку частоти відносяться не до окремого значення ознаки, а до всього інтервалу. Тобто, точні, конкретні значення ознаки залишаються невідомими, оскільки частота показує кількість елементів вибірки, у яких ознака, що вивчається, приймає значення в межах певного інтервалу.

Для зручності подальшого опрацювання статистичних даних, зображених інтервальними статистичними рядами, “представником” інтервалу вважають його середину. Крім цього, замість абсолютних значень частот тут використовують відносні величини, тобто відносні частоти Qi (i = 1, l).

таблиці даних, згрупованих за частотою або за відносною частотою називають статистичними рядами згрупованих даних.

У таблиці 1.2 зображено інтервальний статистичний ряд розподілу похибок при визначенні діаметра лімба.

Таблиця 1.2

Зауважимо, що кожному інтервалу належить тільки один з його кінців (правий або лівий). У таблиці 1.2 інтервалу належить лівий кінець.

Для вибору оптимальної довжини інтервалу, тобто такої, при якій статистичний ряд не буде громіздким та в ньому не зникатимуть особливості явища, рекомендовано формулу Стерджеса

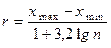. (3.2)

Наприклад, обсяг вибірки n = 200, найбільша варіанта xmax = 85,3, а найменша – xmin = 79,6. Тоді

.

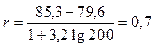Найпростішими інтервальними статистичними рядами є ряди з однаковими довжинами інтервалів (такий зображено таблицею 1.2). Але можна будувати ряди і з різними довжинами інтервалів.

Якщо частоти (коли вони є відомими, як в таблиці 1.2) неперервного статистичного ряду поставити у відповідність серединам інтервалів, то отримаємо дискретний розподіл, який відповідає даному неперервному.

Для неперервних розподілів, особливо тих, які мають різні довжини інтервалів, важливу роль відіграє частота, яка припадає на одиницю довжини інтервалу. Дана величина називається густиною розподілу на цьому інтервалі і визначається формулою

. (1.3)

Така густина називається абсолютною. Якщо скласти відношення відносної частоти до довжини інтервалу, то отримаємо відносну густину розподілу

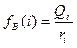. (1.4)

Іноді необхідно знати кількість елементів сукупності, у яких значення ознаки менші за деяку величину. Наприклад, за рядом (див. Табл.3.1) розподілу лімбів різного діаметру кількість їх з діаметром меншим за: 80 мм – 4, 81 мм – 9, 82 мм – 19 і т.д. Таким послідовним сумуванням частот, починаючи з першої варіанти і закінчуючи останньою, ми отримаємо ряд нагромаджених частот, який показує долю елементів сукупності, у яких ознака, що нас цікавить, менша за дане значення.

Всі розглянуті методи організації та зберігання статистичних даних приводять до побудови статистичного розподілу вибірок деякої досліджуваної ознаки.

Аналогічно теорії ймовірностей універсальною та узагальненою формою статистичного розподілу є емпірична функція розподілу.

Емпіричною функцією розподілу (функцією розподілу вибірки) називають функцію F*(x), яка визначає для кожного значення х відносну частоту події (X < x), тобто

, (1.5)

де mx– кількість варіант менших за х; n – обсяг вибірки.

Різниця між емпіричною і теоретичною функціями розподілу полягає в тому, що теоретична функція F(x) визначає ймовірність події (X < x), а емпірична функція F*(x) відносну частоту цієї ж події. Теорема Бернуллі закону великих чисел говорить, що частота події (X < x) прямує за ймовірністю до ймовірності цієї події при необмеженому зростанні обсягу вибірки, тобто емпірична функція за числовими значеннями мало відрізняється від теоретичної. Тому емпірична функція розподілу вибірки може оцінювати теоретичну функцію розподілу генеральної сукупності.

емпірична функція F*(x) має такі ж властивості як і теоретична функція F(x). Наведемо їх.

1. Всі значення емпіричної функції належать відрізку [0;1] .

2. F*(x) – неспадна функція.

3. Якщо x1– найменша варіанта, тоді

F*(x) = 0 для x £ x1,

а якщо x2– найбільша варіанта, тоді

F*(x) = 1 для x > x2.