Перевірка гіпотези про рівність дисперсій двох нормально розподілених генеральних сукупностей

Перевірка таких гіпотез в геодезичній практиці пов’язана з порівнянням характеристик точності геодезичних інструментів та різних методів спостережень. Очевидно, що кращим буде той метод чи інструмент, який забезпечує найменше розсіювання результатів вимірювань.

Розглянемо гіпотезу про рівність дисперсій двох нормально розподілених генеральних сукупностей. Для перевірки такої гіпотези необхідно знати таку функцію їх статистичних оцінок, розподіл якої не залежав би від будь-яких невідомих параметрів. Такій умові задовольняє розподіл відношення двох незміщених оцінок дисперсій, отриманих із незалежних вибірок

. (6.66)

Вираз (3.66) використовують у випадку, коли математичні сподівання вибірок є невідомими. Якщо математичні сподівання вважаються відомими, тоді використовують зміщені оцінки дисперсій

. (6.67)

У більшості практичних випадків використовують вираз (3.66) і вибирають його так, щоб у чисельнику знаходилось число більше, ніж у знаменнику. Величина F має F – розподіл (Фішера–Снедекора). Цей розподіл, як відомо, залежить тільки від кількості ступенів довільності k1 = n1– 1 і k2 = n2– 1 (n1, n2– обсяги вибірок, із яких знайдено оцінки першої і другої дисперсій відповідно).

Сформулюємо гіпотезу про рівність дисперсій двох нормально розподілених генеральних сукупностей.

Нехай сукупності X і Y розподілені нормально. За незалежними вибірками з обсягами n1 і n2, відібраними з цих сукупностей, знайдено виправлені вибіркові дисперсії s20xі s20y. Необхідно за виправленими дисперсіями та за вибраним рівнем значущості a перевірити нульову гіпотезу H0: D(X) = D(Y). Через те, що виправлені вибіркові дисперсії є незміщеними оцінками, нульову гіпотезу можна записати так:

H0: M[s20x] = M[s20y].

Така задача ставиться тому, що, як правило, вибіркові дисперсії є різними. Тому виникає запитання, чи суттєво відрізняються між собою вибіркові дисперсії.

Якщо станеться так, що нульова гіпотеза справедлива (генеральні дисперсії є однаковими), тоді різниця між виправленими дисперсіями є незначною, що пояснюється випадковими причинами (наприклад, випадковим відбором об‘єктів вибірки). Припустимо, що різниця виправлених вибіркових дисперсій результатів вимірювань, виконаних двома різними методиками, виявилася незначною. Це означає, що методики забезпечують однакову точність результатів.

Якщо нульова гіпотеза буде відхилена (генеральні дисперсії є різними), тоді і різниця між вибірковими дисперсіями є значною (суттєвою) і не може пояснюватися випадковими причинами, а є наслідком того, що генеральні дисперсії в дійсності є різними. Це значить, що точність застосованих методик різна і треба вибрати точнішу.

Перевірка гіпотези про дисперсії виконується за тим самим порядком, який встановлений для перевірки раніше розглянутих гіпотез.

Статистичним критерієм перевірки гіпотези про рівність дисперсій двох нормально розподілених генеральних сукупностей є величина F, подана виразом (3.66). Графік розподілу цього критерію для типових значень k1і k2зображено на рисунку 3.12. Критична область будується в залежності від вигляду конкуруючої гіпотези.

Рис. 6.12

Розглянемо перший випадок, коли нульовою гіпотезою є Н0: D(X) = D(Y) а конкуруючою – Н1: D(X) > D(Y). У цьому випадку будують правобічну критичну область, для якої

.

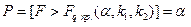Критичну точку Fq пр.(a, k1, k2) знаходять із таблиці критичних точок розподілу Фішера–Снедекора (k1– кількість ступенів довільності більшої дисперсії (див. Додаток, табл. 5).

Тоді правобічна критична область визначатиметься нерівністю

,

а область прийняття гіпотези такою нерівністю:

Якщо обчислене значення критерію за формулою (3.66) є Fобч.< Fq пр., то немає підстав відхиляти нульову гіпотезу.

Якщо Fобч.> Fq пр., то нульову гіпотезу відхиляють.