Метод Стокса

Формула Стокса (2.2) позволяет определить коэффициент вязкости h, если известны другие величины. Метод определения коэффициента вязкости с помощью уравнения (2.2) называется методом Стокса.

Рассмотрим падение шарика в вязкой жидкости. При движении шарика слой жидкости, граничащий с его поверхностью, прилипает к шарику и движется со скоростью шарика, поэтому различные слои отличаются по скорости, и возникает сила вязкого трения.

На шарик, падающий в вязкой жидкости, действуют три силы (рис.2.2):

1)cила тяжести F₁ = mg = r Vg;

2)cила Архимеда F₂ = r_жVg (равная весу жидкости в объеме шарика);

3) сила вязкого трения, обусловленная вязкостью жидкости F₃ =6ph rv.

Здесь r- плотность материала шарика; r_ж - плотность жидкости; V – объем шарика; g - ускорение свободного падения. Все три силы направлены по вертикали: F₁ - вниз, F₂ и F₃ - вверх.

В общем случае уравнение движения ша­ри­ка имеет вид

 

F₁ - F₂ - F₃ = m dv/dt.(2.3)

Поскольку сила вязкого трения, действующая на шарик, зависит от скорости, то ускорение dv/dt уменьшается до тех пор, пока шарик не достиг такой скорости v₀, при которой ускорение равно нулю. Тогда уравнение (2.3) примет вид:

(r - r_ж ) Vg - 6ph r v₀ = 0 . (2.4)

В этом случае шарик движется с постоянной скоростью v₀.

Решая уравнение (2.4) относительно h, по­лу­чим

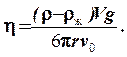(2.5)

Если теперь учесть, что V = 4/3 p r³, r = d/2, v₀ = l / t, где d – диаметр шарика; l- длина участка равномерного движения, пройденного за время t, то формула (2.5) примет окончательный вид:

. (2.6)

Таким образом, для нахождения h нужно измерить d, l и t.