Доведення. Для доведення теореми розглянемо два невід’ємних раціональних числа і , де m, n, p, q – натуральні числа

Для доведення теореми розглянемо два невід’ємних раціональних числа 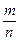і 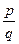, де m, n, p, q – натуральні числа. Згідно означення операції множення 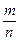• 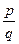= 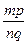. За умовою m,n,p,qєN, а тому mp і nq – також натуральні числа. Отже, добутки mp і nq існують і єдині. Саме тому дробове число існує і єдине. Теорему доведено.

Теорема 2: операція множення невід'ємних раціональних чисел підкоряється комутативному та асоціативному законам, а з операцією додавання пов’язана дистрибутивним законом.

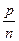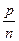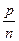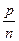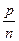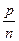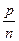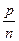Символічно цю теорему можна записати так: 1) (" ÎQ₀)(" ÎQ₀)( • = • ), де , ÎQ₀, - переставна (комутативна) властивість множення; 2) (" ÎQ₀)(" ÎQ₀)(" сÎQ₀)(( • )× = ( × )), де , , ÎQ₀, – сполучна (асоціативна) властивість множення; 3) ("ÎQ₀)("ÎQ₀)("ÎQ₀)((+)• = • + • ), де ,,ÎQ₀, розподільна (дистрибутивна) властивість множення відносно додавання.