
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Доведення.
Розглянемо три дробових числа, але для спрощення викладок виберемо їх із спільними знаменниками,  і доведемо, що (
і доведемо, що (  ). (
). (  =(Чому?!)=
=(Чому?!)=  (Чому?!)=
(Чому?!)=  (Чому?!)=
(Чому?!)=  . Отже, (
. Отже, (  ) сполучний закон додавання невід’ємних раціональних чисел доведено.
) сполучний закон додавання невід’ємних раціональних чисел доведено.
Означення: сума натурального числа і дробового числа, записаних поряд без знака додавання називають мішаним числом.
Наприклад, 8+  =8
=8  . Щоб представити мішане число дробовим, його необхідно перетворити у неправильний дріб, а саме: 8
. Щоб представити мішане число дробовим, його необхідно перетворити у неправильний дріб, а саме: 8  =
=  =
=  . Щоб перетворити неправильний дріб у мішане число, потрібно поділити чисельник на знаменник і частку записати перед дробом, а остачу записати у чисельнику, залишивши той самий знаменник, наприклад:
. Щоб перетворити неправильний дріб у мішане число, потрібно поділити чисельник на знаменник і частку записати перед дробом, а остачу записати у чисельнику, залишивши той самий знаменник, наприклад:  . Отже, множина невід’ємних раціональних чисел замкнена відносно операції додавання.
. Отже, множина невід’ємних раціональних чисел замкнена відносно операції додавання.
Операцію віднімання у множині невід’ємних раціональних чисел також означатимемо так, щоб це не суперечило правилам віднімання цілих чисел.
Означення: відняти від дробового числа 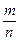 дробове число
дробове число 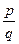 - це означає знайти таке дробове число
- це означає знайти таке дробове число 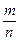 -
- 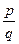 , яке у сумі з дробовим числом
, яке у сумі з дробовим числом 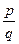 дає нам дробове число
дає нам дробове число 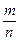 .
.
Таке означення не суперечить тому, яке ми прийняли для невід’ємних цілих чисел. Для того, щоб знайти різницю двох дробових чисел, приймемо наступне означення.
Означення: різницею двох дробових чисел з рівними знаменниками називається таке третє дробове число, чисельник якого дорівнює різниці чисельників, а знаменник – спільному знаменнику.
Символічно прийняте означення запишеться так: 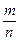 -
-  =
=  . Щоб знайти різницю дробових чисел з різними знаменниками, слід звести їх до спільного знаменника та використати попереднє означення. Символічно це запишеться так:
. Щоб знайти різницю дробових чисел з різними знаменниками, слід звести їх до спільного знаменника та використати попереднє означення. Символічно це запишеться так: 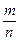 -
- 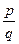 =
= 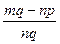 . У прийнятих означеннях нічого не говориться про існування та єдиність різниці. Саме тому слід довести наступні теореми.
. У прийнятих означеннях нічого не говориться про існування та єдиність різниці. Саме тому слід довести наступні теореми.
Теорема: різниця двох невід’ємних раціональних чисел 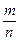 і
і 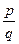 існує тоді і тільки тоді, коли
існує тоді і тільки тоді, коли 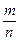 ³
³ 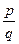 .
.
Дата добавления: 2014-12-03; просмотров: 301; Мы поможем в написании вашей работы!; Нарушение авторских прав |