АНАЛІЗ НЕЛІНІЙНОІЇ САК

В функціональній схемі (додаток 1, рис. 1.1) підсилювач сигналу з виходу вимірювального мосту може мати нелінійну залежність .

В якості нелінійного елементу (НЕ) може бути один із стандартних типів (частина 3, табл. 3.1.), де позначено вхідну величину через , а вихідну через для спрощення запису.

Згідно з завданням (додаток 1), НЕ є трипозиційною релейною характеристикою з зоною нечутливості (рис. 3.1).

рис. 3.1.

Тоді структурну схему системи керування можна представити у вигляді

Рис. 3.2.

де у якості передатної функції лінійної частини системи використовуємо передатну функцію лінійної системи до корекції
(7, додаток 1): .

1. Вихідними даними для визначення параметрів автоколивань за методом Гольдфарба приймаємо передатну функцію лінійної системи до корекції (7, додаток 1) з урахуванням коефіцієнта підсилення, що приходиться на долю нелінійного елементу (рис. 3.1), тобто:

, (49)

та НЕ, зображений на рис. 3.1., для якого згідно з даними таблиці 3.2. (частина 3)

; . (50)

Для початку знайдемо дійсну та уявну частини частотної передатної функції лінійної частини системи :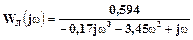

; (51)

. (52)

Змінюючи частоту від нуля до нескінченності, будуємо АФЧХ лінійної частини системи (рис. 3.3). Наступним кроком є побудова у тій же системі координат годографа функції (при зміні ). Результат наведений на рис. 3.3. Так як ці годографи перетинаються, то в НСАК можливі автоколивання, з частотою, що визначається з АФЧХ лінійної частини системи, та амплітудою, що визначається з функції у точці перетину годографів.

Рис. 3.3.

Знайдемо параметри цих автоколивань. За умови , знаходимо частоту автоколивань з рівняння (52): . Вона дорівнює . Підставимо значення цієї частоти у вираз дійсної частини передатної функції лінійної частини системи (51): . Підставимо це значення у функцію , та знайдемо амплітуду можливих автоколивань: .

Для багатозначних нелінійностей можлива наявність двох точок перетину годографів (рис. 3.4).

Якщо годограф НЕ виходить з охвату АФЧХ лінійної частини, то точка 2 визначає амплітуду та частоту стійких автоколивань в системі. Якщо годограф НЕ входить в охват (точка 1), то НСАК нестійка.

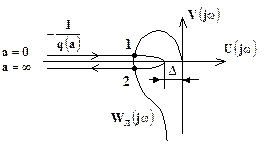
Рис. 3.4.

2. Вихідними даними для визначення абсолютної стійкості НСАК за критерієм В.М. Попова приймаємо передатну функцію лінійної системи до корекції (7, додаток 1) з урахуванням коефіцієнта підсилення, що приходиться на долю нелінійного елементу (рис. 3.1), тобто:

.

Так як НЕ має зону нечутливості та насичення, ми маємо змогу досліджувати наявну астатичну систему.

Для початку знайдемо модифіковані дійсну та уявну частини частотної передатної функції лінійної частини системи використовуючи вирази (51) та (52):

; (53)

. (54)

Змінюючи частоту від нуля до нескінченності, будуємо АФЧХ модифікованої лінійної частини системи (рис. 3.5).

Згідно з критерієм Попова (Гелига) коефіцієнт нахилу прямої 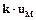(рис. 3.1) повинен бути , тобто . Обираємо .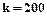

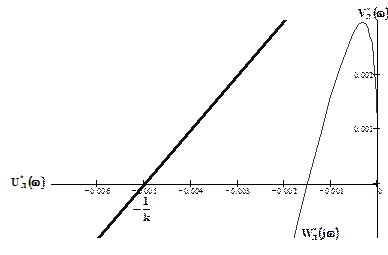
Рис. 3.5.

Так як пряма, що проходить через точку не перетинає годограф модифікованої лінійної частини системи, то НСАК знаходиться в стані абсолютної стійкості.