
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
АНАЛІЗ ДИСКРЕТНОІ САК
Проведемо аналіз дискретного аналога отриманої скорегованої лінійної САК, використовуючи її передатну функцію (29, додаток 1):
 .
.
1. Визначимо період дискретизації імпульсного елементу  з умови теореми Котельникова:
з умови теореми Котельникова:  , де
, де 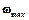 – частота, на якій рівень коефіцієнта підсилення розімкнутої системи на порядок нижчий, ніж на частоті зрізу, де сигнал проходить через систему без змін. На цій частоті можна вважати, що вихідний сигнал майже відсутній, тому вибір періоду дискретизації за таких умов не повинен значно впливати на роботу дискретного аналогу системи. Для визначення частоти
– частота, на якій рівень коефіцієнта підсилення розімкнутої системи на порядок нижчий, ніж на частоті зрізу, де сигнал проходить через систему без змін. На цій частоті можна вважати, що вихідний сигнал майже відсутній, тому вибір періоду дискретизації за таких умов не повинен значно впливати на роботу дискретного аналогу системи. Для визначення частоти 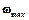 скористаємось наступним рівнянням:
скористаємось наступним рівнянням:  , або
, або 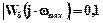 . Аналітичний розв’язок цього рівняння складає великі труднощі, тому скористаємось можливостями програмного пакету MATHCAD:
. Аналітичний розв’язок цього рівняння складає великі труднощі, тому скористаємось можливостями програмного пакету MATHCAD:
 . (37)
. (37)
Тоді період дискретизації повинен бути  .
.
На вибір періоду дискретизації накладають ще одне обмеження – він повинен буди рівним або меншим за найменшу сталу часу, яка характеризує динамічні властивості лінійної неперервної частини дискретної системи. В нашому випадку період дискретизації повинен бути  . Обираємо його значення, що дорівнює
. Обираємо його значення, що дорівнює  .
.
2. Знайдемо передатну функцію розімкненої дискретної системи за формулою:
 . (38)
. (38)
Для виконання Z-перетворення необхідно вираз у дужках розкласти на елементарні дроби. Ми зробимо це за допомогою можливостей програмного пакету MATHCAD:
 .
.
За допомогою таблиць перетворення [7, ст. 252] перейдемо від s-форми до z-форми:


Зробивши спрощення виразу, отримаємо:
 . (39)
. (39)
Тоді передатна функція замкненої дискретної системи буде мати вигляд:
 (40)
(40)
а передатна функція замкнутої дискретної системи за похибкою виглядає так:
 . (41)
. (41)
3. Визначимо стійкість дискретної системи за критерієм Гурвіца. Для цього використаємо характеристичне рівняння передатної функції дискретної замкненої системи:
 (42)
(42)
Для використання критерію Гурвіца необхідно провести білінійне перетворення виду:  .
.
Для цього за допомогою засобів програмного пакету MATHCAD проведемо заміну, та спрощення виразу:
 ,
,
або
 . (43)
. (43)
На основі коефіцієнтів характеристичного рівняння побудуємо визначник Гурвіца за наступною схемою:
 . (44)
. (44)
Згідно з критерієм Гурвіца, система буде стійкою, якщо при 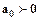 діагональні мінори визначника Гурвіца будуть додатними (для дискретної системи вірно також доповнення, що знак визначників діагональних мінорів повинен співпадати зі знаком коефіцієнта
діагональні мінори визначника Гурвіца будуть додатними (для дискретної системи вірно також доповнення, що знак визначників діагональних мінорів повинен співпадати зі знаком коефіцієнта  , так як в деяких випадках дискретних систем
, так як в деяких випадках дискретних систем  може буди від’ємним):
може буди від’ємним):
 ;
;
 , тобто
, тобто
 ;
;
 .
.
Звідси випливає, що система є стійкою. Це означає, що період квантування вибрано вірно, так як тільки він впливає на стійкість дискретної системи за умови стійкості її лінійної частини.
4. Для визначення запасів стійкості дискретної системи, побудуємо псевдо-частотні ЛАХ та ЛФХ на основі використання переданої функції розімкненої системи (39):
 .
.
Для виконання необхідно провести білінійне перетворення виду: 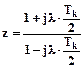 , де
, де 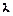 – псевдо-частота.
– псевдо-частота.
Для цього за допомогою засобів програмного пакету MATHCAD проведемо заміну, та спрощення виразу:

Коефіцієнт підсилення псевдочастотної передатної функції дискретної системи майже не відрізняється від коефіцієнту підсилення вихідної лінійної системи, що свідчить про те, що вибір періоду дискретизації імпульсного елементу зроблено коректно. На основі декілька спрощеної псевдо-частотної передатної функції (деякі постійні часу форсуючих та інерційних ланок мають практично однакові значення):
 (45)
(45)
побудуємо її ЛАХ та ЛФХ (рис. 2.1).
Спочатку знаходимо контрольну точку  , з якої буде починатися побудова ЛАХ, за формулою:
, з якої буде починатися побудова ЛАХ, за формулою:
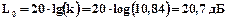 .
.
Далі знаходимо спряжену частоту, як зворотне значення постійної часу:  .
.
Фазова характеристика, згідно з [7, ст. 106] визначається наступною формулою:
 .
.
Так як фазова характеристика не перетинає рівень  , то запас стійкості за амплітудою визначається постійним рівнем вихідного сигналу в області високих частот, тобто
, то запас стійкості за амплітудою визначається постійним рівнем вихідного сигналу в області високих частот, тобто  .
.
Для визначення запасу стійкості системи за фазою, необхідно визначити частоту зрізу, тобто частоту на якій ЛАХ перетинає вісь частот. Частота зрізу знаходиться вирішенням рівняння 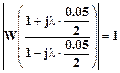 за допомогою засобів програмного пакету MATHCAD:
за допомогою засобів програмного пакету MATHCAD:
 . (46)
. (46)
На частоті зрізу 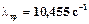 фаза має значення
фаза має значення  , звідси запас стійкості по фазі дорівнює
, звідси запас стійкості по фазі дорівнює 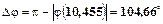 .
.

Рис. 2.1.
5. Для визначення показників якості динамічних властивостей дискретної системи побудуємо її перехідну характеристику (рис. 2.2), використовуючи передатну функцію бажаної системи (29, додаток 1)
 ,
,
за допомогою можливостей програмного пакету MATLAB, виконавши наступні дії:
| >> num=[106.920 10.692] num = 106.920 10.692 | Введення поліному чисельника передатної функції розімкнутої скорегованої лінійної системи Результат введення |
| >> den=[1.958 47.512 166.952 1 0] den = 1.958 47.512 166.952 1.000 0 | Введення поліному знаменника передатної функції скорегованої розімкнутої лінійної системи Результат введення |
| >> W=tf(num,den) Transfer function: 106.9 s + 10.69 ----------------------------------------------- 1.958 s^4 + 47.51 s^3 + 167 s^2 + s | Знаходження передатної функції розімкнутої лінійної системи за допомогою функції “tf” |
| >> Wz=c2d(W,0.05) Transfer function: 0.0008547 z^3 + 0.001722 z^2 – 0.002092 z – 0.0004656 ----------------------------------------------------------------------- z^4 – 3.176 z^3 + 3.649 z^2 – 1.771 z + 0.2973 Sampling time: 0.05 | Знаходження передатної функції розімкнутої дискретної системи за допомогою функції “c2d” та періодом дискретизації 0,05 с. |
| >> Fz=feedback(Wz,1,-1) Transfer function: 0.0008548 z^3 + 0.001722 z^2 - 0.002092 z - 0.0004656 -------------------------------------------- z^4 - 3.175 z^3 + 3.651 z^2 - 1.772 z + 0.2968 | Знаходження передатної функції замкнутої дискретної системи |
| >> step(Fz,35) | Побудова перехідного процесу в дискретній системі протягом 35 с за допомогою функції “step” (рис. 2.2) |

Рис. 2.3.
З рис. 2.3 знаходимо, що час регулювання вихідного параметра (температури в печі) дорівнює  , що відповідає технічному завданню. Відносне перерегулювання знаходимо за формулою:
, що відповідає технічному завданню. Відносне перерегулювання знаходимо за формулою:
 , що також відповідає технічному завданню.
, що також відповідає технічному завданню.
6. Останнім кроком аналізу системи є знаходження усталеної похибки в системі, яка з одного боку залежить від динамічних властивостей системи, з іншого – від форми сигналу на вході системи.
Так як в системі регулювання температури в печі вхідним сигналом є ступінчастий сигнал, то усталену похибку системи слід шукати з використанням так званих коефіцієнтів похибки:
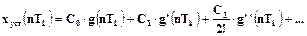 (47)
(47)
Одним з варіантів знаходження коефіцієнтів помилки є використання похідних від передатної функції замкненої системи за похибкою (41), яка в нашому випадку дорівнює:
 .
.
Попередньо зробивши заміну  , коефіцієнти помилки визначається за виразом:
, коефіцієнти помилки визначається за виразом:
 (48)
(48)
Використовуючи можливості програмного пакету MATHCAD знайдемо дві перші похідні від передатної функції за похибкою, що дозволить нам знайти три перших коефіцієнта помилки:
 ;
;
 ;
;
 .
.
Приймаючи, що задана температуру у печі дорівнює  , отримуємо усталену помилку у системі:
, отримуємо усталену помилку у системі:
 .
.
Дата добавления: 2014-12-23; просмотров: 297; Мы поможем в написании вашей работы!; Нарушение авторских прав |