За критерієм В.М. Попова визначити абсолютну стійкість НСАК.

Абсолютна стійкість стану рівноваги – це стійкість в цілому для деякого класу нелінійностей, наприклад, для нелінійностей, що лежать у секторі 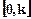,– рис. 3.4, – тобто між віссю х і прямою kx.

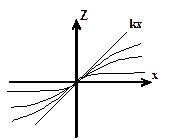
Рис. 3.4. Статичні характеристики нелінійностей.

Метод розроблений у 1959р. румунським математиком В.М. Поповим.

Нелінійна система має абсолютно стійкій стан рівноваги, якщо виконується наступна нерівність:

(3.10)

де – передатна функція лінійної частини системи; – довільне дійсне число, а нелінійна статична характеристика Z лежить в секторі [0,k].

Умови, які накладаються на лінійну частину системи :

1. повинна бути стійкою (всі корені характеристичного рівняння повинні лежати у лівій напівплощині).

2. Система повинна бути статичною та фізично реалізуватися. При цьому виключається з розгляду цілий клас астатичних систем.

Представимо частотну передаточну функцію лінійної частини системи у вигляді суми дійсної та уявної 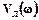складових:

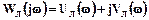(3.11)

З умови абсолютної стійкості НСАК отримаємо:

. (3.12)

Вводимо модифіковану передаточну функція:

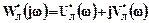, (3.13)

де

; , (3.14)

тоді

. (3.15)

Графічна інтерпретація теореми В.М. Попова (рис. 3.5): якщо можна провести в площині пряму через точку з координатами , що не перетинає амплітудно-фазову характеристику модифікованої системи , то система має абсолютно стійкий стан рівноваги.

Рис. 3.5. Аналіз стійкості НСАК за методом Попова.

Критерій Геліга (розвиток методу В.М. Попова).

Вводяться наступні обмеження на нелінійності:

1. У нелінійності повинні бути наявні зони нечутливості та насичення (рис. 3.6).

2. Нелінійність не повинна прилягати до прямої .

Рис. 3.6. Статичні характеристики нелінійностей.

На відміну від методу В.М. Попова клас лінійних систем розширюється і можуть досліджуватись системи з астатизмом першого порядку. Подальше формулювання критерію ідентичне методу В.М. Попова.