АНАЛІЗ НЕПЕРЕРВНОІ ЛІНІЙНОІ САК

1. На основі рівнянь, що описують динамічні властивості кожного елементу системи, та підставляючи дані з таблиці 1, визначимо їх передатні функції:

– передатна функція мосту:

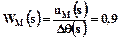; (1)

– передатна функція підсилювача та модулятора:

; (2)

– передатна функція виконавчого двигуна з редуктором:

; (3)

– передатна функція об’єкту керування (печі) описується двома передатними функціями:

а) за вхідним сигналом (переміщенням клапану газопроводу):

; (4)

б) за зовнішнім збуренням:

. (5)

Структурно зв’язок між параметрами, які безпосередньо впливають на зміну вихідної координати (температури) відображено на рис. 1.2, де .

Рис. 1.2. Передатна функція об’єкту керування

2. На основі отриманих передатних функцій елементів системи складаємо структурну схему системи (рис. 1.3).

Рис. 1.3. Структурна схема САК.

3. На основі структурної схеми знайдемо передатні функції, які описуюсь динамічні властивості системи.

Передатна функція розімкнутої системи за вхідним сигналом знаходиться за формулою:

, (6)

тобто

. (7)

Передатна функція замкненої системи за вхідним сигналом буде мати вигляд:

, (8)

де – загальний коефіцієнт підсилення системи, тобто

. (9)

Передатна функція замкненої системи за сигналом похибки , згідно виразу 1.2 (частини 1 даних методичних вказівок) буде мати вигляд

, (10)

або

; (11)

Передатна функція замкненої системи за збуренням , згідно виразу 1.3 (частини 1 даних методичних вказівок) буде мати вигляд

, тобто (12)

або

. (13)

4. Визначимо стійкість замкненої САК за критерієм Гурвіца. Для цього використаємо характеристичний поліном (знаменник передаточної функції) передаточної функції замкненої системи за вхідним сигналом (9):

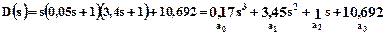.(14)

На основі коефіцієнтів характеристичного поліному побудуємо визначник Гурвіца за наступною схемою:

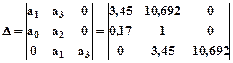. (15)

Згідно з критерієм Гурвіца, система буде стійкою, якщо при 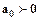діагональні мінори визначника Гурвіца будуть додатними:

;

, тобто ;

.

Звідси випливає, що система є стійкою. Однак даний критерій не дає відповіді, які запаси стійкості має система і чи потребує подальшого вдосконалення для досягнення заданих показників якості.

5. Метод D-розбиття за параметром . Визначимо критичний коефіцієнт підсилення системи, при якому система буде знаходитись на коливальний межі стійкості. Для цього скористаємось частотним методом D-розбиття, який дозволить нам визначити область допустимих значень загального коефіцієнту підсилення системи. Використаємо характеристичне рівняння передатної функції замкненої системи (8) та (9) зі заздалегідь невідомим загальним коефіцієнтом підсилення системи:

. (16)

Визначимо поліном , який не залежить від параметру , та поліном , який залежить від параметру .

Тоді вираз, який визначає невідомий параметр буде мати вигляд:

. (17)

Зробимо заміну 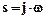, тоді вираз невідомого параметра в частотній формі буде мати вигляд:

. (18)

З цього поліному визначимо дійсну та уявну частину виразу:

, . (19)

Змінюючи частоту з деяким кроком зміни , знаходимо значення та , і на комплексній площині будуємо область допустимих параметрів (рис. 1.6). Так як коефіцієнт підсилення є дійсною величиною, то за умови стійкості системи, вона буде стійкою, якщо коефіцієнт підсилення буде знаходитись у межах .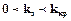

Для більш точного визначення граничного коефіцієнта підсилення проведемо наступні дії – знайдемо точки перетину отриманого графіка з дійсною віссю комплексної площини. Для цього прирівняємо вираз уявної частини (19) до 0: . Вирішимо отримане рівняння , з якого випливає, що графік перетинає дійсну вісь у двох випадках: 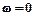та . Підставимо отримані значення у вираз для . Отримаємо , а . Тобто критичний коефіцієнт підсилення системи .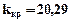

Цей результат також свідчить, що система є стійкою, так як коефіцієнт підсилення системи менший за його критичне значення. Однак питання щодо запасів стійкості системи все ще остається невирішеним.

Рис. 1.6.

6. Визначення запасів стійкості. Для визначення запасів стійкості системи застосуємо критерій Найквіста, в якому використовується передатна функція розімкненої системи за вхідним сигналом (7):

.

Зробимо заміну 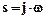, тоді передатна функція в частотній формі буде мати вигляд:

. (20)

Для визначення дійсної та уявної частини частотної передатної функції необхідно помножити її чисельник та знаменник на вираз, спряжений знаменнику відносно уявної частини, з ціллю позбавлення від уявної частини знаменника отриманих виразів:

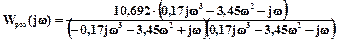. (21)

Спростивши вираз, отримаємо:

. (22)

Звідси випливає:

, .(23)

Змінюючи частоту з деяким кроком зміни , знаходимо значення та , і на комплексній площині будуємо годограф Найквіста (шлях руху вектору, що описує амплітудно-фазочастотні властивості системи з ростом частоти) (рис. 1.7).

Для більш точного визначення точки перетину годографа з дійсною віссю комплексної площини прирівняємо вираз уявної частини (23) до 0: . Вирішимо отримане рівняння , з якого випливає, що годограф перетинає дійсну вісь тільки у випадку: . Підставимо отримане значення у вираз для . Отримаємо .

Рис. 1.7.

Запас стійкості за амплітудою характеризує віддаленість точки АФЧХ від межі стійкості, тобто від точки з координатами –1,j0 (це частота, при якій фаза становить значення 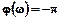, тобто вісь, на який знаходиться ця точка, характеризує границю стійкості системи за фазою). Тоді запас стійкості системи у відносних одиницях дорівнює .

Використовуючи отримане значення, можливо отримати запас стійкості системи за амплітудою, виражений в децибелах: 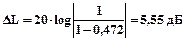. Таким чином, запас по амплітуді являє собою запас за коефіцієнтом передачі розімкнутого ланцюга по відношенню до його граничного за стійкістю значення.

Вираз, за яким змінюється фаза системи визначається за формулою:

. (24)

Для знаходження запасу стійкості системи за фазою, необхідно вирішити наступний рівняння:

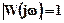. (25)

З виразу (25) ми отримаємо так звану частоту зрізу . Запас стійкості за фазою визначається величиною, на яку має зрости запізнення по фазі в системі з частотою зрізу, щоб система опинилася на межі стійкості.

Аналітичне вирішення рівняння (25) пов’язано з великими труднощами, тому значення частоти зрізу знаходимо за допомогою можливостей програмного продукту MATHCAD:

.

З отриманих результатів знаходження корнів рівняння (25) за частоту зрізу обираємо дійсне додатне значення .

Підставивши в вираз для фази (24) отриману частоту , знайдемо запас стійкості системи за фазою: .

Виходячи з отриманих результатів, робимо висновок, що система є стійкою, але має замалі запаси стійкості по фазі та амплітуді (на практиці, надійно працююча система повинна мати запас за амплітудою та за фазою ), тому потребує подальшої корекції.

7. Для проведення корекції системи для початку нам необхідно побудувати логарифмічні амплітудно-фазочастотні характеристики вихідної системи з використанням передатної функції (7) розімкненої системи за вхідним сигналом:

.

Спочатку знаходимо контрольну точку , яка згідно з (1.5) та (1.6) частини 1 даних методичних вказівок має вигляд:

, (26)

і з якої буде починатися побудова ЛАЧХ.

Далі знаходимо спряжені частоти, як зворотні значення постійних часу: , .

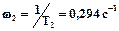Вихідна САК (7) є системою третього порядку з астатизмом першого порядку, до складу якої входить загальний коефіцієнт підсилення системи, інтегруюча ланка (редуктор), інерційна ланка першого порядку, що описує динаміку виконавчого двигуна та інерційна ланка першого порядку, що описує динаміку об’єкта керування (печі). Кожна з цих ланок дає нахил ЛАЧХ у , тобто останній відрізок ЛАЧХ буде мати нахил у (рис. 1.8).

Фазову характеристику згідно з [7, ст. 106] будуємо за формулою:

. (27)

Як бачимо з рис. 1.8, запаси стійкості співпадають зі значеннями, які були розраховані за критерієм Найквіста. Хоча система є стійкої, запаси стійкості замалі, що впливає на якість динамічних процесів у системі (велика ступінь коливань вихідної координати).

8. Так як система має замалі запаси стійкості за фазою та амплітудою, необхідно провести її корекцію. Корекція системи повинна забезпечити необхідні характеристики системи, тобто задані запаси стійкості і показники перехідного процесу.

Так як САК працює на постійному струмі, проведемо корекцію системи за допомогою введення у її склад послідовного коригувальний фільтру у вигляді пасивної RC-ланки.

Побудуємо ЛАЧХ бажаної системи, виходячи з заданих параметрів якості:

– відносне перерегулювання ;

– час регулювання .

Для цього за першою номограмою Солодовнікова (рис. 1.9) визначаємо, що для значення перегулювання , залежність між часом регулювання та частотою зрізу ЛАЧХ бажаної системи має співвідношення: 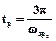. З цього виразу отримуємо, що .

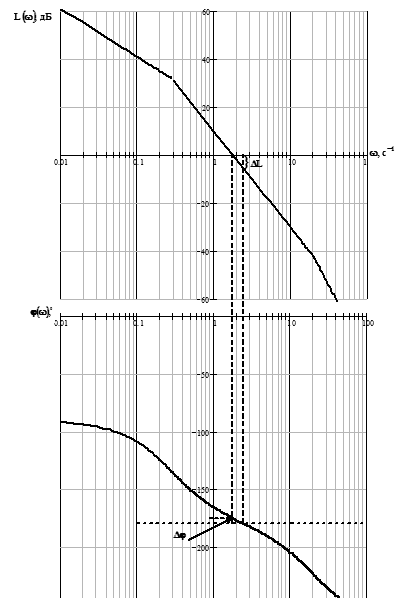
Рис. 1.8.

Рис. 1.9.

Для того, щоб бажана система була стійкою, необхідно, щоб ЛАЧХ перетинала вісь частот під нахилом , причому мінімальний запас стійкості за амплітудою для заданого значення перегулювання повинен бути (за другою номограмою Солодовнікова). За вказаних умов побудуємо ЛАЧХ в області середніх частот у діапазоні під нахилом (рис. 1.10). Починаючи з частоти ЛАЧХ бажаної системи співпадає з ЛАЧХ вихідної системи, та при цьому забезпечується необхідний мінімальний запас стійкості за амплітудою.

Для спряження ЛАЧХ бажаної системи з ЛАЧХ вихідної системи в області низьких частот, з частоти будуємо ЛАЧХ під нахилом до збігу його с ЛАЧХ вихідної системи. Цей збіг проходить на частоті , тобто у діапазоні , ЛАЧХ бажаної (рис. 1.10) та вихідної (рис. 1.8) систем співпадають, та проходять під нахилом .

Рис. 1.10.

За виглядом ЛАЧХ бажаної (скорегованої) системи визначаємо її передану функцію:

, (28)

де

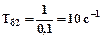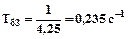, , , тобто:

. (29)

Згідно з [7, ст. 106] ЛФЧХ бажаної системи будуємо за формулою:

.

Визначимо запаси стійкості бажаної системи за амплітудою та фазою.

На частоті зрізу фаза має значення , звідси запас стійкості по фазі дорівнює .

Для того, що знайти запас стійкості за амплітудою скорегованої САК, необхідно спочатку вирішити наступне рівняння:

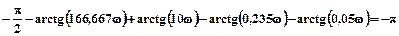.(30)

Знайти аналітично рішення рівняння (30) дуже складно, тому використаємо можливості програмного пакету MATHCAD для знаходження його коренів:

.

З отриманих результатів обираємо дійсне додатне значення частоти 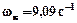та підставляємо його у вираз .

Отримуємо, що запас стійкості бажаної системи за амплітудою дорівнює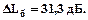

Віднімаючи від ЛАЧХ бажаної системи ЛАЧХ вихідної системи, отримуємо ЛАЧХ послідовного коригувального пристрою (рис. 1.10).

На основі ЛАЧХ послідовного коригувального пристрою (рис. 1.10) визначаємо його передатну функцію:

. (31)

9. За формою ЛАЧХ коригувального пристрою з [9, ст. 643] обираємо схемну реалізацію послідовного коригувального пристрою (рис. 1.11) та використовуємо розрахункові формули.

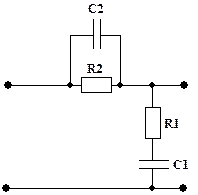
Рис. 1.11.

Де , . Приймаючи , отримуємо: , .

Так яка коригувальний пристрій працює на постійному струмі, то необхідно його включити до схеми після моста перед підсилювачем-модулятором (рис. 1.1).

10. Використовуючи передатну функцію (32) замкненої скоректованої системи за вхідним сигналом, знайдемо перехідну функцію нашої скорегованої системи для визначення показників якості її динамічних властивостей. Зображення перехідної функції знаходимо за виразом: 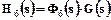, де

, (32)

– зображення за Лапласом вхідного сигналу. Для отримання перехідної функції необхідно на вхід системи подати одиничний ступінчастий сигнал, зображення якого має вигляд . Враховуючи це, вираз для зображення перехідної функції буде мати вигляд:

. (33)

За допомогою можливостей програмного пакету MATHCAD, розкладемо отримане зображення (33) вихідного сигналу на часткові дроби для подальшого знаходження оригіналів елементарних ланок:

.

За таблицями перетворення Лапласа [7, ст. 252] визначаємо оригінал функції (перехідну функцію) скоректованої системи:

(34)

На основі отриманої перехідної функції (34), будуємо перехідну характеристику скорегованої системи (рис. 1.12).

Рис. 1.12.

З рис. 1.12 знаходимо, що час регулювання вихідного параметра дорівнює 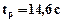, що відповідає технічному завданню (табл. 1). Відносне перерегулювання знаходимо за формулою:

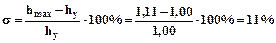, що також відповідає технічному завданню (табл. 1).

11. Останнім кроком аналізу системи є знаходження усталеної похибки в системі, яка з одного боку залежить від динамічних властивостей системи, з іншого – від форми сигналу на вході системи.

Так як в системі регулювання температури в печі вхідним сигналом є сигнал, що повільно змінюється з часом (в більш конкретному випадку це ступінчастий сигнал ), то усталену похибку системи слід шукати з використанням так званих коефіцієнтів похибки:

(35)

Одним з варіантів знаходження коефіцієнтів помилки є використання похідних від передатної функції (11) замкненої системи за похибкою, яка в нашому випадку дорівнює .

В цьому разі коефіцієнти похибки визначається за виразом:

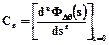(36)

Використовуючи можливості програмного пакету MATHCAD знайдемо дві перші похідні від передатної функції за похибкою, що дозволить нам знайти три перших коефіцієнта похибки:

;

;

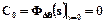, тобто

Приймаючи, що задана температуру у печі дорівнює , отримуємо усталену помилку у системі:

.

Розрахунки підтвердили те, що якщо в систему з астатизмом першого порядку подати сигнал постійної величини, то похибка на виході системи в усталеному режимі буде дорівнювати “0”, тобто усталений вихідний сигнал буде дорівнювати вхідному.

12. Для дослідження впливу різноманітних вхідних сигналів на роботу системи, а також її поведінку під впливом зовнішнього збурення, заданого у завданні до курсової роботи, проведемо моделювання отриманої системи у середовищі Simulink програмного пакету MATLAB. Структурна схема вихідної системи з урахуванням послідовного коригувального пристрою наведена на рис. 1.13.

Рис.1.13.

При подачі на вхід системи одиничного ступінчастого сигналу, вихідний сигнал буде мати вигляд, наведений на рис. 1.14. Цей графік повністю співпадає з результатами розрахунків перехідної функції (п. 10).

Рис. 1.14.

Якщо на вхід системи подати значення температури 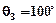(при початковому значенні 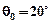), то зміна вихідної величини набуває вигляду, який наведений на рис. 1.15.

Рис. 1.15.

При впливі на систему лінійно зростаючого збурення , яке виникає на 20-й секунді роботи системи, при деяких відхиленнях система все-таки справляється з дією збурення з невеликими змінами у загальному часі регулювання (рис. 1.16).

Рис. 1.16.