Метод гармонійної лінеаризації.

Метод використовується для дослідження автоколивальної стійкості[BMV13] НСАК. За його використанням можливо лінеаризувати будь-який НЕ, одержати його передатну функцію, визначити стійкість НСАК, а також визначити амплітуду та частоту стійких автоколивань в системі, якщо вони присутні.

Розглянемо структурну схему розімкнутої НСАК, зображену на рисунку 3.2.

Рис. 3.2.Структурна схема розімкненої НСАК.

Якщо на вхід НЕ подати гармонійний сигнал: ,то на виході НЕ з’явиться також гармонійний сигнал виду , що є результатом спотворення вхідного сигналу статичною характеристикою НЕ.

Оскільки сигнал є періодичнім, то його можна представити у вигляді ряду Фур’є:

(3.1)

Приймаємо гіпотезу про те, що лінійна частина є фільтром нижніх частот. Це дає можливість для аналізу розглядати у частотному спектрі сигналу лише постійну складову та першу гармоніку. Таким чином, сигнал на вході НЕ можна представити у вигляді суми тільки двох членів ряду, оскільки інші гармоніки не проходять на вихід лінійної частини:

(3.2)

При умові, що НЕ є симетричним, постійна складова ряду Фур’є . Тоді .

Відомо, що , тоді

, (3.3)

де:

;

.

З рівняння отримаємо наступні вирази ; ; . Тоді .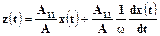

Після введення коефіцієнтів гармонійної лінеаризації , , отримаємо .

В таблиці 3.2. наведені коефіцієнти гармонічної лінеаризації для різних типів НЕ.

Перетворимо за Лапласом .

Звідси передатна функція гармонійно лінеаризованого НЕ має вигляд:

. (3.4)

В частотній формі (при заміні ) передатна функціє НЕ має вигляд:

. (3.5)

Коефіцієнти гармонійної лінеаризації наведені у таблиці 3.2.

Таблиця 3.2.

Коефіцієнти гармонічної лінеаризації нелінійностей

№	Вид нелінійності	Значення ,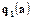
1.		; .
2.		; .

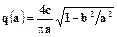Продовження табл. [BMV14] 3.2.

№	Вид нелінійності	Значення ,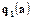
3.		, ; , .
4.		, ; .
5.		, , ; .
6.		.