КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Адсорбция на жидких поверхностях. Изотерма Гиббса.
Для поверхностей раздела между двумя несмешивающимися жидкими фазами существует хорошо измеримая величина, называемая межфазным поверхностным натяжением σ, которая зависит от адсорбции отдельных компонентов на границу раздела. Такая же величина, характеризующая границу раздела жидкость - газ называется просто поверхностным натяжением и относится к жидкости. Молекулы жидкости, находящиеся на поверхности или в её окрестности обладают большей энергией, чем аналогичные молекулы в объёме жидкости. Разность этих энергий на поверхности и в объёме, отнесённая к единице площади поверхности раздела и называется поверхностным натяжением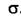 
. Эта величина имеет порядок 
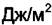. Для воды
при 298 К и является одной из самых больших величин характеризующих вещества, находящиеся в жидком состоянии при стандартных условиях.
Двухфазная термодинамическая система с такой границей раздела будет стремиться к равновесию с минимальной поверхностью раздела. Для такой системы, имеющей объёмы фаз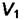 
и 
и 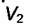поверхность раздела между ними s, давления фаз соответственно 
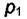и 
можно записать
|
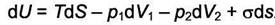
Величина σds - это уменьшение внутренней энергии системы при уменьшении поверхности раздела на ds (ds - отрицательная величина) при эволюции системы к равновесию в условиях S, Vb V2 = const. Очевидно
|
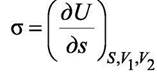
(6.8)
Аналогичным образом можно определить поверхностное натяжение через другие характеристические функции Н, F и G.
Рассмотрим равновесие жидкой и газовой фаз двухкомпонентной системы при постоянных р и Т. Будем считать поверхность раздела плоской и давление в фазах одинаковым. В растворителе содержится нелетучее вещество с объёмной концентрацией с [моль/л]. Газовая фаза содержит только молекулы растворителя. Раствор идеален. Растворённое вещество может адсорбироваться на межфазной границе. Предположим для определённости, что выход вещества на поверхность раздела фаз снижает свободную энергию системы. В равновесии поверхностную концентрацию адсорбированного вещества на границе раздела фаз обозначим через Г [моль/м2], т. е. 
. Не нарушая
равновесия и не изменяя площади поверхности раздела s, уменьшим количество растворённого вещества на dn2, таким образом, изменив его концентрацию в объёме на dc2. Учитывая, что dG = 0 в этих условиях, аналог уравнения Гиббса-Дюгема (5.5) с межфазной поверхностью запишется в виде
где 
и 
количества молей растворителя и растворённого вещества в межфазном поверхностном слое, 
и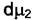 
соответствующие изменения химических потенциалов при изменении объёмной концентрации растворённого вещества на 
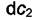Вводя величину 
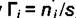, получим
(6.9)
Величина Гi в (6.9), введённая Гиббсом, это избыток числа молей i-го компонента в объёме поверхностного слоя с площадью s = 1м2 по сравнению с числом его молей в таком же объёме, находящимся внутри раствора, где концентрации не меняются от точки к точке. Эта величина называется гиббсовской адсорбциейили адсорбцией компонента "i" у данной поверхности. При малых объёмных концентрациях i-го компонента в объёмной фазе Гi близка к поверхностной концентрации введённой ранее для адсорбции из газа на твёрдую поверхность. Само уравнение (6.9) называется адсорбционным уравнением Гиббса.
Так как 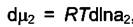 , где а2 - активность растворённого вещества в
объёме раствора
|
Применяя формулу (6.9) к рассматриваемому случаю её можно упростить, если выбрать положение поверхности s таким образом, чтобы величина адсорбции растворителя П = 0. Это всегда можно сделать и положение поверхности не будет меняться в случае малых концентраций с2. Если растворимое вещество ещё и сильно адсорбируется, то положение поверхности, для которой П = 0, не отличается от положения математической поверхности раздела. Тогда (6.9) преобразуется к виду
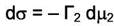
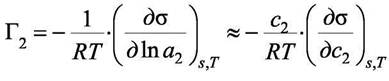
Уравнение (6.10) называется уравнением изотермы адсорбции
Гиббса.Оно позволяет определять адсорбцию Г2 на границе раздела
жидкость - газ по зависимости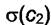 
Для данного растворителя есть вещества, которые снижают
поверхностное натяжение: 
, тогда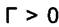 
. Граница раздела фаз обогащается растворённым веществом, и такие вещества называются
поверхностно-активными (ПАВ). Вещества, для которых 
>,0 и
, называются поверхностно-инактивными (неактивными).
Отметим, что формула (6.10) справедлива только в той области концентраций растворённого вещества, когда можно принять коэффициент активности близким к единице. Для растворов неэлектролитов её можно применять до концентраций 0,1 моль/л, а для электролитов - до 0.01 моль/л.
В области малых объёмных концентраций растворённого вещества, так же как и при малых давлениях газа, адсорбция идёт по закону Генри, т.е.
Дата добавления: 2014-12-23; просмотров: 250; Мы поможем в написании вашей работы!; Нарушение авторских прав |