Выборочный метод. Статистическое распределение выборки

Редактор издательства Т.И.Королева

Компьютерный набор Л.А.Карабан

Темплан 2010 г., п. 25

Подписано в печать 23.04.10 Формат 60х84 1/16 Бумага офсетная

Офсетная печать. Печ. л. 7,9. Уч.-изд.л. 7,9 Тираж 80 экз. Заказ

Издательство Брянского государственного технического университета

241035, г. Брянск, бульвар им. 50-летия Октября, 7, БГТУ, 58-82-49

Лаборатория оперативной полиграфии БГТУ, ул. Институтская, 16.

РАЗДЕЛ II. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Выборочный метод. Статистическое распределение выборки

Совокупность всех мысленно возможных объектов данного вида, над которыми проводятся наблюдения с целью получения конкретных значений определенной случайной величины, или совокупность результатов всех наблюдений, проведенных в неизменных условиях над одной из случайных величин, связанных с данным видом объектов, называется генеральной совокупностью (совокупностью объектов, с которых сделана выборка).

Генеральная совокупность может быть конечной или бесконечной, в зависимости от того, конечная или бесконечная совокупность составляющих ее элементов.

Часть отобранных объектов генеральной совокупности или результаты наблюдений над ограниченным числом объектов из этой совокупности называются выборочной совокупностью или выборкой (совокупностью случайно отобранных объектов).

Число N объектов генеральной совокупности и число п объектов выборочной совокупности будем называть объемами генеральной и выборочной совокупностей (число объектов этой совокупности) (N > п).

О свойствах генеральной совокупности можно судить по данным наблюдений над отобранными объектами, то есть выборкой.

Для того чтобы за выборкой можно было довольно уверенно судить о случайной величине, выборка должна быть репрезентативной.

Репрезентативность выборки означает, что объекты выборки довольно качественно представляют генеральную совокупность.

Репрезентативность выборки обеспечивается случайностью отбора.

Операция, которая содержится в том, что наблюдаемые значения случайной величины, располагают в возрастающем (неубывающем) порядке, называется ранжированием статистических данных.

Пример 1. На телефонной станции проводились наблюдение над числом х – неправильных соединений в минуту. Наблюдение в течение часа дали следующие результаты: 3, 1, 3, 1, 4, ....

Расположив эти данные в порядке возрастания и сгруппировав их, получим ранжированный ряд наблюдений:

.

Есть семь разных значений случайной величины:

0, 1, 2, 3, 4, 5, 7.

Каждое такое значение называется вариантой.

Значение случайной величины, которая отвечает отдельной группе сгруппированного ряда наблюдаемых данных, называют вариантой, а последовательность вариант, размещенных в возрастающем порядке – вариационным рядом.

Численность отдельной группы сгруппированного ряда наблюдаемых данных называется частотой варианты.

Отношение частоты данной варианты к общей сумме частот всех вариант называют относительной частотой

,

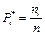где 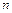– объем выборки.

Относительная частота является статистической вероятностью появления варианты .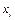

Дискретным вариационным рядом распределения называется ранжированная совокупность вариант 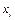с соответствующими им частотами или с относительными частотами.

Иначе говоря, это статистическое распределение выборки.