Точечные оценки параметров распределения

Во многих случаях надо исследовать количественный признак Х генеральной совокупности, используя результаты выборки. Часто для этого достаточно найти приближенные значения математического ожидания 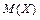, дисперсию , среднее квадратичное отклонение 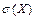, начальные или центральные моменты случайной величины Х.

Иногда из некоторых соображений удается установить закон распределения Х. Тогда надо уметь оценивать параметры это распределения.

Точечная оценка некоторого параметра распределения определяется по данным выборки, характеризуется одним числом и служит оценкой параметра распределения генеральной совокупности.

Приведем основные точечные оценки параметров распределения.

Средним арифметическим наблюдаемых значений случайной величины х называется частное от деления суммы всех этих значений на их количество, то есть

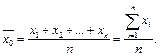
Выборочной среднейназывают среднее арифметическое значение признака выборочной совокупности

где: 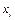– значение i-варианты; – частота варианты; 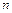– объем выборки; т – число разных вариант.

Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения

.

Если данные наблюдений представлены в виде дискретного вариационного ряда, причем – наблюдаемые варианты, а – соответствующие им частоты, то выборочная дисперсия упрощается, если ее находить по формуле

,

Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии

.

Выборочная дисперсия равна разности между средним арифметическим квадратов наблюдений над случайной величиной х и квадратом ее среднего арифметического, то есть

.

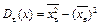Исправленная выборочная дисперсия:

.

Исправленное выборочное среднее квадратичное отклонение:

.

Выборочная асимметрия:

.

Выборочный эксцесс:

.

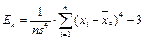Если выборка задана дискретным статистическим рядом

			...
			...

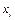
это в этом случае расчетные формулы имеют вид

,

, где ,

,

, .

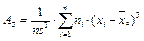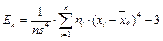Пример 1. В результате пяти измерений длины изделия одним прибором (без систематических погрешностей) получены следующие результаты в мм: 92; 94; 103; 105; 106.

Найти:

а) выборочное среднее длины изделия;

б) выборочную и исправленную дисперсии погрешностей прибора.