Интервальные оценки параметров распределения

Если объем выборки довольно большой, то точечные оценки параметров распределения не удовлетворяют практические нужды точности.

Интервальной называют оценку, которая определяется двумя числами – концами интервала.

Вероятность того, что абсолютная величина отклонения выборочной средней от генеральной средней не превысит положительного числа , называется надежной вероятностью(доверительной вероятностью).

Надежностью (доверительной вероятностью) оценки параметра по называют вероятность

,

с которой выполняется неравенство .

Обычно надежность оценки задается заранее, причем в качестве берут число, близкое к 1. Наиболее часто задают надежность, равную 0,95 или 0,99 или 0,999.

Формулу надежности можно записать в виде

.

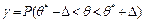Из этого равенства следует, что интервал содержит неизвестный параметр генеральной совокупности.

Интервал называют доверительным, если он покрывает неизвестный параметр с заданной надежностью .

Пусть количественный признак Х генеральной совокупности распределен по нормальному закону, причем среднее квадратичное отклонение этого распределения известно. Надо найти доверительный интервал, который покрывает математическое ожидание генеральной совокупности с заданной надежностью .

Согласно свойству нормально распределенной случайной величины Х имеем

,

где

– функция Лапласа.

Но случайная величина, , поэтому при замене Х на , на получим

,

где

– точность оценки (предельная погрешность),

то есть с надежностью доверительный интервал

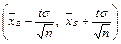
покрывает неизвестный параметр а.

Точность оценки (предельная погрешность) будет

.

Число 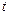определяется из равенства

с использованием таблицы значений интегральной функции Лапласа.

Замечание. Из анализа точности оценки вытекает, что при росте объема выборки п число уменьшается, а это означает, что точность оценки увеличивается. Когда надежность увеличивается, функция возрастает и согласно ее свойством возрастает 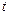и, как следствие, возрастает . Итак, увеличение надежности оценки уменьшает ее точность.