Общие сведения о методе фазовой плоскости

В любой момент времени состояние автоматической системы n-порядка может быть охарактеризовано значениями управляемой величины 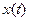и (n-1) ее производных. Это означает, что для этой системы требуется использование n-мерного пространства, содержащего n осей координат. Если для каждого момента времени по указанным осям отложить значение переменной 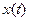и (n-1) ее производных, то будет получена точка, отражающая состояние системы. Указанное пространство является фазовым, а точка, соответствующая состоянию системы, – изображающей точкой (ИТ).

В течение переходного процесса переменная 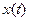и ее производные в каждый момент времени будут иметь различные значения, поэтому ИТ будет из начального положения (задаваемого начальными условиями) перемещаться в фазовом пространстве, при этом каждому типу переходного процесса автоматической системы в фазовом пространстве отвечает определенная траектория движения ее ИТ. В состоянии равновесия ИТ находится в покое, все производные равны нулю – соответствующие точки фазового пространства называются особыми.

Совокупность фазовых траекторий для всех возможных начальных состояний вместе с особыми точками называется фазовым портретом системы.

Наиболее наглядно фазовые траектории могут быть представлены для систем второго порядка, т.е. для таких систем, для которых уравнение динамики записывается в виде:

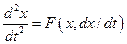, (1.1)

В этом случае фазовое пространство является двумерной плоскостью: по оси абсцисс откладывается регулируемая величина x, а по оси ординат – скорость ее изменения y=dx/dt. Дифференциальное уравнение для фазовых координат можно получить, исключив время из дифференциальных уравнений динамики, записанных в нормальной форме Коши:

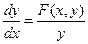. (1.2)

Уравнение фазовой траектории является решением этого дифференциального уравнения. Фазовые траектории имеют следующие особенности: они закручены по часовой стрелке (в верхней полуплоскости ИТ «движется» слева направо, а в нижней – справа налево), пересекают ось абсцисс под прямым углом и не пересекаются нигде, кроме как в особых точках.

Для систем автоматики содержащих нелинейные звенья является нелинейной функцией своих аргументов, поэтому, в общем случае, решение уравнения, для заданных начальных условий, может быть получено с использованием одного из приближенных методов.