Метод припасовывания

Для нелинейных элементов с такими кусочно-линейными характеристиками уравнение (1.2) будет разбиваться на ряд линейных уравнений, каждое из которых будет записываться для своей области фазового пространства. Поэтому для каждой области фазового пространства можно сравнительно просто получить точное решение уравнения (1.2), а далее, полученные фазовые траектории должны быть состыкованы («сшиты») по линиям «переключения», которые определяются характером разрывов и изломов нелинейной зависимости.

«Сшивание» означает, что конечные значения состояния системы для данной области (координаты ИТ на линии переключения) используются в качестве начальных условий для следующей области. Такой метод расчета фазовых траекторий получил название метода припасовывания.

а

б

в

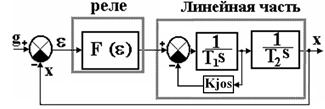
Рис. 1.1. Структурная схема нелинейной системы слежения второго порядка: а – исходная нескорректированная система; б – коррекция характеристик линейной части (охват исполнительного механизма жесткой обратной связью – демпфирование); в – коррекция характеристик с использованием дополнительной гибкой обратной связи (коррекция по скорости или ПД-закон регулирования – ).

Проанализируем методом припасовывания динамику нелинейной системы слежения второго порядка, линейную часть которой составляют 2 последовательно соединенных интегрирующих звена (рис. 1.1). Примером такой системы может являться модель двухпозиционного авторулевого – первому интегрирующему звену соответствует исполнительный механизм, отвечающий за поворот руля, а второму – объект управления (судно).

В первом приближении считаем, что нелинейное звено соответствует идеальному двухпозиционному реле. Тогда дифференциальное уравнение фазовых координат (1.2) запишется для системы без коррекции (рис. 1.1.а) в виде:

, (1.3)

где ,

Это нелинейное уравнение разбивается на два линейных уравнения для областей значений фазовых параметров, лежащих левее и правее линии переключения ε=0 (x=g). При пересечении этой линии значение – правая часть уравнения (1.3) скачкообразно изменяется и, поэтому, фазовая траектория испытывает излом. Наличие в схеме двух последовательно соединенных интегрирующих (звеньев без дополнительных мер демпфирования) определяет нахождение системы на границе колебательной устойчивости.

Фазовая траектория системы в этом случае соответствует замкнутому граничному циклу (особая точка – центр, а переходной процесс – незатухающие колебания). Несложно показать, что амплитуда А (при нулевых начальных условиях) и период Т_кол данных автоколебаний в системе будет рассчитываться по формуле:

, (1.4)

где – величина ступенчатого изменения сигнала задания.

Из выражения (1.4) видно, что для нелинейных систем такой важный параметр такой важный параметр как период свободных колебаний не является постоянным (для линейных систем определяется формулой ), а зависит от уровня входного сигнала.

Для коррекции данной системы можно использовать 2 стандартных приема.

Возможна коррекция линейной части системы путем охвата исполнительного механизма (первого из двух интеграторов) жесткой отрицательной обратной связью (ЖОС). В состав ЖОС входит усилительное (пропорциональное) звено и которая, поэтому, действует как в переходном, так и в установившемся режиме (рис. 1.1.б).

Благодаря действию ЖОС идеальное интегрирующее звено превращается в апериодическое звено первого порядка, что, в свою очередь обуславливает рассеивание (диссипацию) энергии в системе и затуханию колебаний в переходных процессах. Поэтому, такой способ коррекции называется демпфированием. В случае коррекции демпфированием дифференциальное уравнение фазовых координат приобретает вид:

(1.4)

Как видно из уравнения (1.4) увеличение глубины обратной связи (значения ) ведет к уменьшению наклона фазовой траектории, что, в свою очередь определяет уменьшение заброса и колебательности в переходном процессе. При малых значениях увеличение глубины обратной связи ведет к ускорению переходного процесса, но дальнейшее увеличение этого параметра приводит к затягиванию процесса за счет начальной стадии его.

Возможна и коррекция путем использование дополнительной гибкой обратной связи (ГОС), которая действует только в переходных и отключается в установившихся режимах (рис.1.1.в). Очевидно, что в состав ГОС должно входить дифференцирующее звено, что отвечает использованию ПД-закона управления. Такой способ коррекции называется коррекцией по скорости.

Применение ГОС, обеспечивает, как и в случае линейных систем, улучшение показателей качества переходного процесса. Переключение реле происходит, когда величина ошибки (входного сигнал реле) ε=0, но значение ошибки теперь .

Поэтому, при >0, переключение совершается с опережением по сравнению с нескорректированной системой. Заметим, что величина коэффициента передачи по гибкой обратной связи играет роль времени дифференцирования в ПД-законе управления. Уравнение прямой переключения принимает вид:

. (1.5)

Незатухающий переходной процесс сменится затухающим, колебательность и заброс в котором уменьшаются по мере роста величины . Одновременно число колебаний становится конечным и на линии переключения появляется участок, к которому фазовые траектории подходят с обеих сторон, а отходящих траекторий нет.

Причина появления его в том, что чем ближе к оси абсцисс пересекает фазовая траектория линию переключения, тем круче она наклонена к оси абсцисс. Когда ее наклон сравняется с наклоном линии переключения, ИТ будет двигаться по этой линии к точке установившегося режиму ( 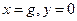) и колебательный процесс будет заканчиваться апериодическим «хвостом». Скорость скольжения ИТ к положению равновесия на этом участке определяется текущей координатой y, т.е. финальная стадия процессов в скользящем режиме будет инвариантна к свойствам объекта и определяться только уравнением линии переключения (скольжения).

Такой режим работы релейной САУ называется скользящим. В режиме скольжения реле тоже конечно должно переключаться, поэтому физически скользящий режим заключается в бесконечно быстрых переключениях реле, вызывающих соответственно колебания с бесконечно малой амплитудой относительно постепенно спадающего к нулю среднего значения. Однако, в реальности колебания получаются большой, но конечной частоты и малой, но конечной амплитуды. Это связано с наличием у реальных релейных элементов петлевой зоны неоднозначности конечной ширины[1]. При наличии конечной ширины зоны гистерезиса линии переключения в верхней и нижней полуплоскостях теперь не совпадают, а смещены на величину ширины зоны неоднозначности. На фазовом портрете это ведет к образованию замкнутых фазовых траекторий, охватывающих точку равновесия, – граничных циклов.

Специфические изменения в фазовых траекториях и графиках переходных процессов возникают при наличии у реле зоны нечувствительности (трехпозиционное реле). В этом случае метод припасовывания также применим для расчета процессов в системе, однако фазовую плоскость следует разбивать не на 2, а на 3 области, разделяемых двумя линиями переключения. Эти линии будут одновременно наклоняться при использовании дополнительной корректирующей ГОС. При наличие зоны нечувствительности на фазовом портрете вместо особой точки появляется особый отрезок, к которому подходят все фазовые траектории и появляется статическая ошибка САУ, величина которой пропорциональна ширине зоны нечувствительности.