
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретическая часть. Если порядок нелинейной системы превышает второй, то описание динамики системы путем нахождения решения системы нелинейных дифференциальных уравнений является
Если порядок нелинейной системы превышает второй, то описание динамики системы путем нахождения решения системы нелинейных дифференциальных уравнений является слишком громоздким и, зачастую, неэффективным. На практике часто применяется приближенный метод, который сводится к замене нелинейного уравнения линейным, а далее полученное дифференциальное уравнение исследуется обычными методами линейной теории. В отличие от предыдущей работы производимая замена одинакова для всех областей фазового пространства, т.е. эффекты переключения не рассматриваются.
Если входящий в систему элемент характеризуется несущественной нелинейностью (отсутствуют разрывы или изломы) статической характеристики, то допустима процедура статической линеаризации (разложение в ряд Тейлора с отбрасыванием старших членов ряда). Для существенной нелинейности такая процедура замены недопустима и должна зависеть от уровня входного сигнала, т.е. может фактически плавно изменяться по ходу переходного процесса.
В последнем случае чаще всего приходится рассчитывать параметры периодических движений – колебаний. Дело в том, что кроме ситуаций, когда система находится под действием источника периодических внешних возмущений, в нелинейных системах зачастую встречается случай, когда в ней самой самовозбуждаются и самоподдерживаются периодические процессы. Такие процессы называются автоколебаниями.
Автоколебания отличаются от свободных незатухающих колебаний консервативных линейных систем (систем без потерь энергии, т.е. без «трения») и возникают в существенно неконсервативных системах. Они самовозбуждаются за счет флуктуаций (случайных изменений) входного сигнала и поддерживаются за счет равенства потерь энергии за колебательный цикл и притока энергии от неколебательного источника. При этом автоколебания не исчезают при изменениях параметров системы и (или) начальных условий (т.е. не превращаются ни в затухающие, ни в расходящиеся колебания).
Изучение автоколебаний весьма существенно, поскольку, с одной стороны, в распространенных системах автоматического регулирования, содержащих двух- или трех позиционные релейные регуляторы, автоколебания отвечают нормальному режиму работы. С другой стороны, автоколебания могут являться нежелательным фактором, который ухудшает качество процессов в системе, снижает точность, поэтому требуется применение мер для их подавления.
Физическая причина возникновения автоколебаний заключается в следующем. Для многих нелинейных элементов малое входное воздействие усиливается значительно, а большой входной сигнал, благодаря эффекту насыщения, усиливается слабо или ослабляется. Поэтому при флуктуационном увеличении амплитуды автоколебаний эффективный коэффициент усиления разомкнутой системы уменьшается, замкнутая система становится устойчивой и колебания начинают затухать. При уменьшении же амплитуды автоколебаний процесс идет в противоположную сторону, так что единственно возможным остается существование колебаний со строго определенной амплитудой, отвечающей границе устойчивости системы.
Для анализа колебательных процессов в нелинейных системах используется приближенный метод, основанный на разложении в ряд Фурье с отбрасыванием старших слагаемых ряда. Он получил название метода гармонической линеаризации(ГЛ).
Идея метода ГЛ заключается в следующем:
Пусть на вход элемента с существенно нелинейной статической характеристикой 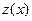 (НЭ) поступает входной гармонический сигнал
(НЭ) поступает входной гармонический сигнал 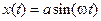 . Сигнал на выходе
. Сигнал на выходе 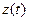 сохраняет периодичность изменения, но искажается сравнительно с входным синусоидальным сигналом (теряет гармоничность).
сохраняет периодичность изменения, но искажается сравнительно с входным синусоидальным сигналом (теряет гармоничность).
Известно, что любая периодическая функция может быть представлен в виде суммы гармонических слагаемых (гармоник) частоты которых кратны основной частоте, называемой первой гармоникой (теорема Фурье):
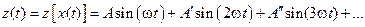 , (2.1)
, (2.1)
где  – амплитуды соответствующих гармоник.
– амплитуды соответствующих гармоник.
Однако в системах автоматического управления обычно последовательно с нелинейным элементом включено линейное звено (линейный фильтр – ЛФ), как показано на рис. 2.1. Оно тем сильнее ослабляет амплитуду колебаний, чем выше их частота (т.е. чем выше номер гармоники, тем сильнее она подавляется). Такой частотной характеристикой (т.н. фильтр низких частот) обладают инерционные и интегрирующие звенья, из которых обычно и состоит линейная часть.
Поэтому, если частота входного гармонического сигнала достаточно большая, то можно считать, что на выходе линейного фильтра сохраняется только одна первая гармоника (основная частота, совпадающая с частотой входного сигнала). Математически это означает, что выходной сигнал должен быть разложен в ряд Фурье с отбрасыванием всехслагаемых (гармоник разложения), кроме первой. В этом и заключается приближенность метода.
 Рис. 2.1. Прохождение гармонического сигнала через нелинейный элемент и
линейный фильтр
Рис. 2.1. Прохождение гармонического сигнала через нелинейный элемент и
линейный фильтр
|
Таким образом, на выходе ЛФ остаётся фактически гармонический сигнал, а поэтому можно периодический негармонический сигнал 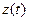 заменить на сигнал первой гармоники
заменить на сигнал первой гармоники 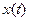 , т.е. мысленно заменить НЭ на безынерционный линейный элемент с коэффициентом передачи (коэффициентом ГЛ):
, т.е. мысленно заменить НЭ на безынерционный линейный элемент с коэффициентом передачи (коэффициентом ГЛ):
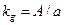 , (2.2)
, (2.2)
где 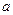 – амплитуда гармонического сигнала на входе в НЭ,
– амплитуда гармонического сигнала на входе в НЭ,  – амплитуда первой гармоники на выходе НЭ.
– амплитуда первой гармоники на выходе НЭ.
Фактически главнейшим отличием метода ГЛ от обычных методов линеаризации нелинейной статическойхарактеристики (например методом касательной)является то, что величина коэффициента передачи 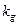 зависит от амплитуды входного сигнала, т.е. для каждого значения величины a требуется произвести новую замену. Величину
зависит от амплитуды входного сигнала, т.е. для каждого значения величины a требуется произвести новую замену. Величину 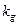 можно рассчитать, используя разложение в ряд Фурье, а можно измерить экспериментально.
можно рассчитать, используя разложение в ряд Фурье, а можно измерить экспериментально.
Расчет 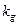 для некоторых НЭ представлен в табл. 2.1. Убывающие функции
для некоторых НЭ представлен в табл. 2.1. Убывающие функции 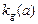 , представленные в таблице, показывают возможность возникновения в системе автоколебаний.
, представленные в таблице, показывают возможность возникновения в системе автоколебаний.
Табл. 2.1. Гармоническая линеаризация некоторых однозначных нелинейностей
| Тип нелинейности | Формула коэффициента ГЛ |
| Идеальное двухпозиционное реле | 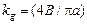
|
| Идеальное трехпозиционное реле | 
|
| Насыщение | 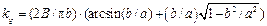
|
Если статическая характеристика нелинейного элемента является неоднозначной (петлевой), то вследствие эффекта запаздывания в передаче сигнала в ряде Фурье (2.1) следует кроме синусоидальных слагаемых учитывать и косинусоидальные члены. Это, в свою очередь, означает, что приближенное представление нелинейного элемента должно учитывать наличие двух коэффициентов гармонической линеаризации.
Для экспериментального определения коэффициента ГЛ по формуле (2.2) необходимо знать амплитуду первой гармоники A, поскольку амплитуда, подаваемого входного сигнала а, известна. Величину А можно вычислить, зная передаточную функцию линейного фильтра  , и, измерив амплитуду гармонических колебаний А1 на выходе его:
, и, измерив амплитуду гармонических колебаний А1 на выходе его:
 . (2.3)
. (2.3)
Тогда получаем:
 .
.
Выбрав единичную амплитуду подаваемого входного сигнала а, окончательно получаем:
 . (2.4)
. (2.4)
Экспериментальные значения 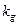 находимые по формуле (2.4), будут отличаться от значений, которые рассчитаны по формулам представленным в табл. 2.1. Чем выше частота входного сигнала ω, тем эффективнее работа фильтра низких частот линейного элемента по подавлению старших гармоник и тем ближе получаются измеренные и теоретически рассчитанные значения. Поэтому обоснованность применения приближенного метода ГЛ тем выше, чем большими фильтрующими свойствами обладает линейная часть системы.
находимые по формуле (2.4), будут отличаться от значений, которые рассчитаны по формулам представленным в табл. 2.1. Чем выше частота входного сигнала ω, тем эффективнее работа фильтра низких частот линейного элемента по подавлению старших гармоник и тем ближе получаются измеренные и теоретически рассчитанные значения. Поэтому обоснованность применения приближенного метода ГЛ тем выше, чем большими фильтрующими свойствами обладает линейная часть системы.
Автоколебания с конечной амплитудой могут развиться в замкнутой системе, если порядок линейной части ее не ниже третьего, поскольку такая система может находиться в состоянии, лежащем на границе колебательной устойчивости. Для возбуждения автоколебаний на вход системы может подаваться периодический, произвольный непериодический сигнал, а в некоторых случаях автоколебания самовозбуждаются даже в отсутствии какого-либо входного сигнала. Именно этот случай рассматривается в лабораторной работе, поскольку для него наиболее просто произвести расчет параметров автоколебаний. Структурная схема системы, соответствующей данному случаю представлена на рис. 2.2.
 Рис. 2.2. Структурная схема системы, в которой самовозбуждаются автоколебания
Рис. 2.2. Структурная схема системы, в которой самовозбуждаются автоколебания
|
К исследованию линеаризованной системы можно применить весь аппарат линейной теории управления, и, в частности, критерии устойчивости. Передаточная функция разомкнутой гармонически линеаризованной системы может быть записана в виде:
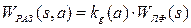 . (2.5)
. (2.5)
Для нахождения системы на границе устойчивости, согласно критерию Найквиста, необходимо выполнение соотношения:
 , (2.6)
, (2.6)
или иначе:
 (2.7)
(2.7)
Гольдфарб предложил решить это соотношение графически, строя отдельно на комплексной плоскости годограф АФЧХ 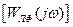 линейной части и обратную амплитудную характеристику
линейной части и обратную амплитудную характеристику 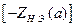 нелинейного элемента. Точки пересечения их и являются решением данного уравнения (рис. 2.3а).
нелинейного элемента. Точки пересечения их и являются решением данного уравнения (рис. 2.3а).
 а
а
|  б
б
|
| Рис. 2.3. Метод Гольдфарба определения параметров автоколебаний. Нелинейная статическая характеристика: а – неоднозначная, б – однозначная. |
При этом точкам пересечения 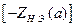 и
и 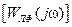 соответствуют автоколебания с частотой
соответствуют автоколебания с частотой  , определяемой по АФЧХ
, определяемой по АФЧХ 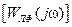 линейной системы и амплитудой а, определяемой по характеристике
линейной системы и амплитудой а, определяемой по характеристике 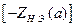 . Если же характеристики не пересекаются, то автоколебания отсутствуют, и САУ является абсолютно устойчивой.
. Если же характеристики не пересекаются, то автоколебания отсутствуют, и САУ является абсолютно устойчивой.
В частном случае, если статическая характеристика нелинейного элемента однозначная, то первая гармоника выходного сигнала совпадает по фазе (синхронна) с входным сигналом (т.е. в разложении Фурье не содержится косинусоидальной составляющей) и  совпадает с осью абсцисс (рис. 2.3б) и характеристика
совпадает с осью абсцисс (рис. 2.3б) и характеристика 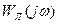 в точках пересечения с характеристикой
в точках пересечения с характеристикой 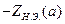 может принимать только действительные значения. Частота колебаний ωа находится при этом из условия
может принимать только действительные значения. Частота колебаний ωа находится при этом из условия 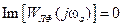 , а амплитуда – из условия
, а амплитуда – из условия 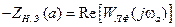 .
.
Дата добавления: 2014-12-23; просмотров: 343; Мы поможем в написании вашей работы!; Нарушение авторских прав |