
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Синтез из структур, одинаковых по характеру устойчивости
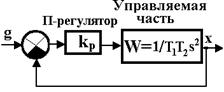
На рис.3.1а представлена структурная схема системы, которая находится в состоянии границы колебательной устойчивости. Здесь  – постоянные времени нейтрального объекта и исполнительного механизма, динамика которых отвечает идеальным интегрирующим звеньям. Коэффициент передачи П-регулятора постоянен и равен kp. Тогда передаточная функция замкнутой системы будет иметь вид:
– постоянные времени нейтрального объекта и исполнительного механизма, динамика которых отвечает идеальным интегрирующим звеньям. Коэффициент передачи П-регулятора постоянен и равен kp. Тогда передаточная функция замкнутой системы будет иметь вид:

В системе наблюдаются незатухающие гармонические колебания, а фазовая траектория имеет одну особую точку – центр. Получим уравнение фазовой траектории.
 а
а
|  б
б
|
| Рис. 3.1. Структурные схемы САУ: а – исходная система с постоянной структурой; б – модифицированная система с переменной структурой. |
Положим, что сигнал задания g=0[4], а свободное движение происходит за счет ненулевых начальных условий системы. В этом случае уравнение фазовой траектории примет наиболее простой вид:
 , (3.1)
, (3.1)
где  – циклическая частота незатухающих колебаний, С – константа, которая определяется начальными условиями системы. Выражение (3.1) является уравнением эллипса с центром в начале координат фазовой плоскости.
– циклическая частота незатухающих колебаний, С – константа, которая определяется начальными условиями системы. Выражение (3.1) является уравнением эллипса с центром в начале координат фазовой плоскости.
При пересечении оси ординат фазовые траектории отсекают, согласно соотношению (3.1), отрезки  , а при пересечении оси абсцисс –
, а при пересечении оси абсцисс –  . Поэтому при ω>1 (α-структура) фазовые траектории вытянуты вдоль оси ординат и имеют вид представленный на рис. 3.2а, а при ω<1 (β-структура) вытянуты вдоль оси абсцисс и представлены на рис. 3. 2б, соответственно.
. Поэтому при ω>1 (α-структура) фазовые траектории вытянуты вдоль оси ординат и имеют вид представленный на рис. 3.2а, а при ω<1 (β-структура) вытянуты вдоль оси абсцисс и представлены на рис. 3. 2б, соответственно.
Заметим, что ИТ, двигаясь по фазовым траекториям, может приближаться или удаляться от точки равновесия  . Так для α-структуры приближение к точке равновесия происходит в первом и третьем квадрантах (когда выполняется условие
. Так для α-структуры приближение к точке равновесия происходит в первом и третьем квадрантах (когда выполняется условие  ), а для β-структуры – во втором и четвертом квадрантах (при условии
), а для β-структуры – во втором и четвертом квадрантах (при условии 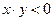 ), как это показано на рис. 3.2в и 3.2г, соответственно[5].
), как это показано на рис. 3.2в и 3.2г, соответственно[5].
Поэтому, если выбрать коэффициент передачи согласно правилу:
 , (3.2)
, (3.2)
 а
а
|  б
б
|
 в
в
|  г
г
|
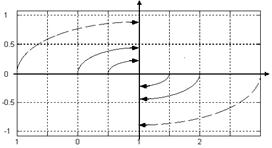
Рис. 3.2. Фазовый портрет САУ для различных настроек регулятора: а – 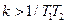 (α-структура); б – (α-структура); б –  (β-структура); в, г – «хорошие» участки фазовых траекторий этих структур. (β-структура); в, г – «хорошие» участки фазовых траекторий этих структур.
|
то можно взять от каждого фазового портрета нужную часть и, составив эти части вместе, получить фазовый портрет системы с устойчивым состоянием равновесия. Фазовая траектория будет представлять собой ломаную скручивающуюся спираль с особой точкой типа устойчивый фокус.
Для реализации отбора нужных частей фазовых портретов необходимо настроить соответствующим образом работу ψ-ячейки, как это представлено на рис. 3.1б.
Очевидно, что в данном случае входные сигналы ψ-ячейки определяются выражениями:
 .
.
Поэтому при пересечении линий  коэффициент передачи (а значит и величина управляющего воздействия) скачкообразно изменяется в соответствии с условием (3.2). Регулируемая величина
коэффициент передачи (а значит и величина управляющего воздействия) скачкообразно изменяется в соответствии с условием (3.2). Регулируемая величина 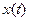 изменяется при этом непрерывно как это представлено на рис. 3.3.
изменяется при этом непрерывно как это представлено на рис. 3.3.
 Рис. 3.3. Переходные процессы в СПС при переключении между состояниями на границе устойчивости
Рис. 3.3. Переходные процессы в СПС при переключении между состояниями на границе устойчивости
|
Эффект транспортного запаздывания в системе будет сказываться на том, что переключения будут происходить не при пересечении вышеуказанных линий переключения, а позже. Поэтому наличие звена ИТЗ в канале передачи управляющего воздействия ухудшает качество процессов в системе. Строго говоря, оба состояния системы в этом случае являются неустойчивыми. Однако, и теперь, при определенных условиях (соотношении между временем запаздывания τ и величинами коэффициентов 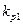 и
и  ) система будет являться устойчивой. Это соответствует тому, что «хорошие» участки фазовых траекторий, представленных на рис. 3.2. в,г, являются теперь не эллипсами, а раскручивающимися спиралями, однако, характеристики спиралей остаются такими, что ИТ, двигаясь по ним, может приближаться к точке равновесия.
) система будет являться устойчивой. Это соответствует тому, что «хорошие» участки фазовых траекторий, представленных на рис. 3.2. в,г, являются теперь не эллипсами, а раскручивающимися спиралями, однако, характеристики спиралей остаются такими, что ИТ, двигаясь по ним, может приближаться к точке равновесия.
Дата добавления: 2014-12-23; просмотров: 262; Мы поможем в написании вашей работы!; Нарушение авторских прав |