Синтез из структур, различных по характеру устойчивости

Рассмотрим функционирование системы, в которую входит устойчивый объект первого порядка и интегрирующий исполнительный механизм, а также пропорциональный регулятор. ψ-ячейка в системе изменяет знак коэффициента передачи k_p, что фактически соответствует изменению знака обратной связи. Система с положительной обратной связью (k_p<0) является естественно неустойчивой.

Физический смысл эффекта переключения знака обратной связи связан с тем, что неустойчивая система является более быстрой, «энергичной» сравнительно с задемпфированной устойчивой системой. Поэтому, выбирая из переходного процесса в неустойчивой системе такие интервалы времени, на которых значение регулируемого параметра стремится к установившемуся значению, можно ускорить переходной процесс.

Структурная схема данной системы представлена на рис. 3.4.

а	б
Рис. 3.4. Структурные схемы САУ: а – исходная система с постоянной структурой; б – модифицированная система с переменной структурой

В данном случае, поскольку положительная обратная связь соответствует неустойчивому состоянию, то ψ-ячейка будет осуществлять переключения между устойчивой α- и неустойчивой β-структурами. В зависимости от того, в каком месте фазового пространства в данный момент времени находится ИТ (т.е. от соотношения знаков функции ошибки и функции переключения ) будет реализовываться устойчивая или неустойчивая структура системы.

Области существования α- и β-структур показаны на рис. 3.5. Здесь в качестве фазовых координат выбраны отклонение и скорость его изменения – .

При изменении знака x₁ или происходит изменение знака их произведения и, соответственно, скачкообразное переключение структуры. Заметим, что знак изменяется при пересечении линии G,уравнение которой:

. (3.3)

Фактически, сравнительно с предыдущим случаем, линия переключения G больше не совпадает с осью абсцисс фазовой плоскости и отклоняется от нее. Отклонение тем меньше, чем больше постоянная времени регулятора 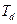, т.е. при линия переключения стремится занять положение, совпадающее с осью абсцисс, а если 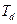=0, то она совпадает с осью ординат.

Рис. 3.5. Разделение фазовой плоскости на области структур разного состояния устойчивости

Передаточная функция замкнутой системы, имеющая свой смысл только для отдельных фиксированных структур (устойчивой или неустойчивой), будет записываться в виде:

, (3.4)

где разные знаки перед слагаемыми в знаменателе отвечают различным типам структур.

Выражение для корней характеристического уравнения будет записываться в виде:

. (3.5)

Знак минус в дискриминанте квадратного уравнения отвечает α-структуре системы, а плюс – β-структуре. В случае α-структуры (при достаточно большом значении k_p) корни уравнения являются комплексно-сопряженными с отрицательной вещественной частью, так что переходной процесс является колебательно-затухающим и фазовая траектория представляет собой спираль, скручивающуюся к точке равновесия (особая точка – устойчивый фокус). В случае β-структуры оба корня уравнения – действительные, при этом один – положительный, а другой – отрицательный, что соответствует фазовому портрету с особой точкой типа «седло».

В этом фазовом портрете особую роль играют линии, разделяющие различные режимы движения, – т.н. сепаратриссы. График фазового портрета с особой точкой указанного типа представлен на рис. 3.6. Одна из сепаратрисс S_y ( ) соответствует фазовой траектории устойчивого вырожденного движения, а вторая S_н ( )– неустойчивого вырожденного движения.

Рис. 3.6. Фазовый портрет системы с особой точкой типа седло и линии сепаратрисс

Возможные режимы работы системы зависят от взаимного расположения линий переключения Gи линии устойчивого вырожденного движения S_y.

1. Вырожденный режим реализуется, если положения этих линий совпадают. Из сравнения (3.3) и (3.5) видно, что условие реализации этого режима – настройка времени дифференцирования на значение:

. (3.6)

Этот режим дает апериодические переходные процессы с максимальным для квазилинейных систем быстродействием. Однако, такой вид режима является неустойчивым, поскольку при сколь угодно малых (флуктуационных) изменениях свойств системы он переходит либо в режим переключений, либо в скользящий режим.

2. Режим переключений реализуется, если линия переключения лежит выше линии устойчивого вынужденного движения. Этому режиму отвечает заниженное значение настроечного параметра ψ-ячейки: . Переходные процессы являются колебательными, однако имеют лучшие показатели качества, чем в аналогичной линейной САУ. Частота переключений в этом режиме сравнительно невысока.

3. Режим скольжения реализуется, если линия переключения лежит ниже линии устойчивого вынужденного движения. Этому режиму отвечает завышенное значение настроечного параметра ψ-ячейки: . Как и ранее (лаб. работа №1) управление по производной (гибкая обратная связь) в релейных системах ведет к появлению эффекта скольжения.

Этому режиму отвечают апериодические переходные процессы. ИТ после попадания на линию переключения скользит вдоль нее к точке покоя фазовой плоскости. Эта линия является линией разрыва фазовых траекторий α- и β-структур, а частота переключений теоретически стремится к бесконечности (а в реальности просто высока и определяется шириной зоны неоднозначности реального реле).

Заметим, что финальная стадия процессов в скользящем режиме будет инвариантна к свойствам объекта и определяться только уравнением линии переключения (скольжения) G. Положение линии S_yможет изменяться при дрейфе параметров объекта, поэтому, чтобы избежать колебательности и обеспечить хорошее качество процесса, требуется задавать наклон линии G таким, чтобы скользящий режим сохранялся всегда.

Если в системе существует эффект транспортного запаздывания, то переход ИТ на новую фазовую траекторию будет отставать от момента переключения на время τ. Если величина τ сравнительно невелика, то скользящий режим сохраняется, поскольку переход происходит до пересечения линии S_y. При этом рыскания ИТ по отношению к линии переключения будут достаточно большими, поэтому такой режим называют квазискользящим. Если же время ИТЗ превышает некоторое критическое значение τ_кр, то переход ИТ на новую фазовую траекторию происходит уже после пересечения линии S_y и наблюдается режим переключений.