Теоретическая часть. Дискретной(во времени)САУназывается такая система, которая кроме непрерывных звеньев содержит хотя бы одно дискретное звено

Дискретной(во времени)САУназывается такая система, которая кроме непрерывных звеньев содержит хотя бы одно дискретное звено, преобразующее непрерывный сигнал в последовательность импульсов определенной формы. Дискретное звено является звеном импульсного действия.

В данной лабораторной работе рассматриваются дискретные системы с амплитудно-импульсной (АИ) модуляцией. В таких системах через равные интервалы времени Т генерируются импульсы фиксированной длительности, амплитуда которых соответствует величине входного аналогового сигнала в момент создания импульса. Идея амплитудно-импульсной модуляции непрерывного сигнала представлена на рис. 4.1.

Рис. 4.1. Идея амплитудно-импульсной модуляции.

При составлении математической модели дискретной системы в ней выделяют непрерывную часть (обычно объект управления и, возможно, исполнительный механизм) и импульсное звено. Далее реальное импульсное звено представляют формально состоящим из двух фиктивных частей – идеального импульсного элемента и формирующего элемента. Такое представление оказывается удобным для создания математической модели системы.

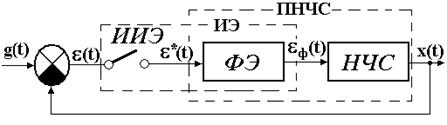
Обычно импульсный элемент в дискретных системах расположен после сравнивающего устройства, так что дискретизируется сигнал ошибки и управление непрерывной частью системы представляется в виде последовательности импульсов. Поэтому структурная схема имеет вид представленный на рис. 4.2.

Рис. 4.2. Структурная схема дискретной системы с АИ модуляцией. Составные части реального импульсного элемента (ИЭ): идеальный импульсный элемент (ИИЭ) и формирующий элемент (ФЭ), НЧС – непрерывная часть системы.

Идеальное импульсное звено образует последовательность мгновенных импульсов (δ-импульсов Дирака), которые следуют один за другим с периодом квантования Т и имеют площадь равную значениям входного сигнала в дискретные моменты времени. Второй же элемент формирует реальные импульсы заданной формы и длительности.

Непрерывную часть системы совместно с формирующим элементом называют приведенной непрерывной частью системы (ПНЧС) или импульсным фильтром (ИФ). При анализе работы импульсного фильтра его входной и выходной сигналы рассматривают в дискретные моменты времени t=nT, т.е. непрерывные функции x(t) и ε(t) заменяют соответствующими им решетчатыми x[n] и ε[n].

Для вычисления значений сигналов в моменты времени t внутри интервала квантования t=nТ+δT применяют смещенные решетчатые функции x[n,δ] и ε[n,δ].

Использование решетчатых функций позволяет корректно описать динамику дискретных систем с использованием не дифференциальных, а т.н. разностных уравнениями, которые связывают решетчатые функции сигналов ошибки, управляющего действия и регулируемой величины. Для их решения над решетчатыми функциями производят Z-преобразование (или модифицированное Z-преобразование), которые являются аналогами преобразования Лапласа для непрерывных систем:

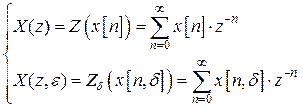, (4.1)

Выполнение дискретного Z-преобразования над разностным уравнением, позволяет получить алгебраическое уравнение вида:

. (4.2)

Здесь – дискретная передаточная функция разомкнутой системы. Зная ее, можно определить передаточную функцию замкнутой системы:

. (4.3)

Если импульсный элемент генерирует прямоугольные импульсы с периодом квантования Т и длительностью Т_и=γТ, где γ=(1-δ) – относительная длительность импульса, то передаточная функция формирующего элемента может быть записана в виде:

.

Поэтому выражение для дискретной передаточной функции ИФ записывается следующим образом:

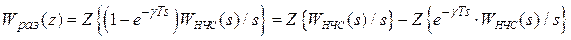
Последний член в этой формуле может быть преобразован с использованием модифицированного Z-преобразования, так что окончательно получаем:

(4.5)

Табл. 4.1 содержит выражения примеры обычного и модифицированного Z-преобразований.

Табл. 4.1. Преобразования некоторых простейших функций

Преобразование непрерывных функций	Преобразование решетчатых функций
Оригинал	Преобразование Лапласа	Оригинал	Простое Z-преобразование	Модифиц. Z-преобразование

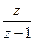
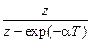
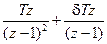
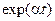
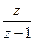
Рассмотрим два случая , отвечающих различному виду непрерывной части системы:

– идеальное интегрирующее звено ;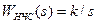

– апериодическое звено первого порядка .

В первом случае, после несложных преобразований можно получить:

, (4.6а)

а во втором:

. (4.6б)

Проиллюстрируем, например, процедуру получения выражения (4.6а). В соответствии с формулой (4.5) получим:

.

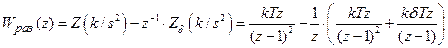Приводя к общему знаменателю и упрощая, получаем:

Аналогично (только более громоздко) можно получить соотношения (4.6б).

Рассмотрим процедуру расчета переходного процесса в исследуемой дискретной системе.

Как видно из формул (4.6) выражение для дискретной передаточной функции замкнутой системы в каждом из случаев сводится к соотношению:

, (4.7)

где а и b – константы, определяемые свойствами НЧС и настройкой импульсного элемента, и – Z-образы входного (обычно ступенчатого) воздействия и выходной (регулируемой) величины.

Уравнение (4.7) может быть преобразовано к виду:

.

Учитывая, что умножение Z-образа функции на z^-k соответствует смещению решетчатой функции оригинала на k тактов в сторону отставания, запишем разностное уравнение для решетчатых функций, которое позволит рассчитать переходной процесс:

(4.8)

Рассмотрим применение рекуррентной схемы решения. Рекуррентный метод заключается в том, что каждый последующий шаг выводится на основе расчета предыдущего. В качестве примера выберем значения параметров а=0,5 и b=0,8. Рекуррентную процедуру будем проводить, записывая результаты вычислений на каждом шаге в таблицу 4.2. Будем считать, что входное воздействие реализует ступенчатую функцию Хевисайда.

Табл. 4.2. Результаты рекуррентного расчета переходного процесса

n
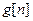
			0,5	0,1	0,42	0,164	0,369	0,205	0,336	0,231	0,315
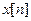
		0,5	0,1	0,42	0,164	0,369	0,205	0,336	0,231	0,315	0,248

Результат расчета обычно включает в себя столько шагов, чтобы достаточно близко подойти к установившемуся значению выходной величины, которая может быть найдена по правилу:

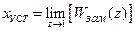(4.9)

В приведенном примере:

,

поэтому расчет охватывает практически все время протекания переходного процесса (т.е. 10 шагов достаточно!).

Для исследования устойчивости дискретной системы по ее передаточной функции необходимо, как и в случае непрерывных систем, определить положения ее полюсов. Импульсная система является устойчивой, если все полюсы дискретной передаточной функции замкнутой системы лежат внутри единичного круга, т.е. выполняется . Часто для исследования на устойчивость применяется билинейное v-преобразование, которое отображает внутренность единичного круга на левую полуплоскость:

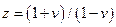. (4.10)

После проведения его анализ устойчивости проводится так же, как и в случае непрерывных систем (применимы необходимое и достаточное условие устойчивости непрерывных систем и известные косвенные критерии устойчивости).

Несложно показать, что в первом случае (в непрерывной части системы идеальное интегрирующее звено) параметры системы должны удовлетворять неравенству:

, (4.11а)

а во втором случае несложное, но громоздкое преобразование, приводит к неравенству вида:

. (4.11б)

Важной особенностью импульсных систем является возможность получения в них переходных процессов конечной длительности, Процессами конечной длительности называют такие процессы, которые заканчиваются за конечное время – конечное число периодов квантования (или конечное число тактов) За один такт – для НЧС первого порядка, за два такта – для НЧС второго порядка и т.д. Для многих (но далеко не для всех!) систем можно добиться протекания переходного процесса конечной длительности одним лишь изменением параметров системы[6]. Для этого все полюсы передаточной функции замкнутой системы в Z-плоскости должны быть равны нулю, т.е. передаточная функция должна иметь вид:

.

В этом случае переходной процесс закончится за k тактов.

В первом случае нулевой корень уравнения получается, если параметры системы удовлетворяют соотношению:

, (4.12а)

а во втором случае:

. (4.12б)

Нелинейные алгебраические соотношения (4.11б) и (4.12б) могут быть решены численно.