
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Введите вектор параметров импульсной системы S, используемых для настройки на нужный режим
Первые 2 компонента вектора S, отвечают значениям двух из трех ("gamma", "T", "k") параметров, вводимых в заданной последовательности
третий компонент может принимать значения 1, 2 или 3. При этом 1 – отвечает поиску gamma", 2 – поиску "T", 3 – поиску "k".
S=[0.8 7.5 2]
Величина периода квантования при настройке на границу устойчивости T_kr=1.048
Величина периода квантования при настройке на режим кон. длительности T_opt=0.46936
Таким образом, если время квантования составляет 1,0480 с, то импульсная система находится на границе колебательной устойчивости, а если – 0,4694 с, то настроена на процесс конечной длительности (оптимальна по быстродействию).
Далее необходимо, настроив соответствующим образом каждый из блоков модели промоделировать протекание процессов в системе.
Исследуйте, как изменяются характеристики процессов (для любого из видов НЧС) при варьировании времени квантования и коэффициента усиления. Результат подтвердите графиками. Сделайте вывод.
Сравните найденные критические и оптимальные настройки для двух видов НЧС. Сделайте вывод.
Поясните отличия в характере процесса конечной длительности при включении в непрерывную часть интегрирующего и апериодического звеньев.
Во второй части работы рассчитывается переходной процесс в импульсной системе, у которой НЧС – идеальное интегрирующее звено, все значения параметров системы соответствуют найденным значениям для границы устойчивости за исключением коэффициента передачи интегрирующего звена – его величина выбирается по формуле 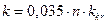 . Далее следует:
. Далее следует:
· записать выражение для дискретной передаточной функции разомкнутой и замкнутой, используя формулы (4.6а) и (4.6б);
· рассчитать установившееся значение по формуле (4.9);
· составить рекуррентное разностное уравнение (4.8);
· составить таблицу, аналогичную приведенной таблице пошагового расчета 4.2;
· провести расчет переходного процесса в S-модели с соответствующими параметрами;
· используя результаты моделирования, сохраненные в память программы, построить график в среде Matlab так, чтобы сравнить найденные значения с результатами расчета S-модели.
Для этого, следует построить график в среде Matlab так, чтобы отдельные отсчеты «отстояли» друг от друга на интервал времени квантования. Это можно осуществить правильным указанием шага выборки из массива, который записан в память программы. Построение графиков следует выполнять без соединения линиями символов, фиксирующих отдельные отсчеты. Такой график будет в наиболее наглядной форме представлять поведение решетчатой функции x[n]. Далее необходимо указать координаты каждой из «дискрет» на плоскости графика, используя функции контекстного меню объекта figure(открытого окна графика Matlab), и, в заключение, сравнить с результатами пошагового расчета.
Так, например сравним результаты рекуррентного расчета с непосредственным моделированием дискретной системы в пакете Simulink при заданном значении времени квантования модели Т=0,2 с. Результаты записывались в двухколоночный массив R. Шаг времени расчета модели (Max step size) составлял 0,01 с, поэтому шаг выборки составляет 0,2/0,01=20 и синтаксис команды имеет вид:
plot(R(1:20:201,1),R(1:20:201,2),'ko').
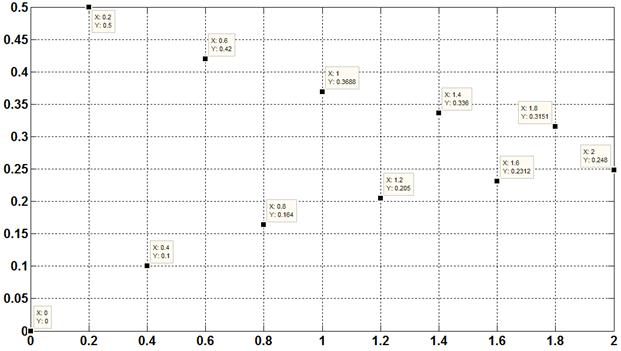 Рис. 4.6. Результаты моделирования переходного процесса в пакете Simulink.
Рис. 4.6. Результаты моделирования переходного процесса в пакете Simulink.
|
Результаты моделирования представлены на рис. 4.6. Для каждого из значений переходной функции непосредственно на графике указаны значения ее координат. Для этого в режиме Data Cursor (на панели Figure Toolbar) по каждой из точек графика производился щелчок ЛКМ при нажатой клавише Alt. Как видно из рис. 4.6 результаты моделирования совпадают с данными, приведенными в табл. 4.2.
В отчете должны быть представлены:
· структурная схема исследуемой импульсной системы;
· результаты расчета варьируемого параметра, соответствующего двум режимам работы импульсной системы (распечатку диалогового окна выполнения файла-сценария включать не следует!);
· переходной процесс в системе при настройке на два этих режима;
· анализ изменения переходного режима при изменениях варьируемых параметров системы;
· выражение для передаточной функции замкнутой системы с вычисленными значениями параметров;
· таблица результатов рекуррентного расчета переходного процесса с подтверждением в виде графика моделирования его;
· письменный ответ на вопросы, указанные преподавателем.
Контрольные вопросы
1. Какие системы называются дискретными? Из каких элементов состоят импульсные системы с АИ-модуляцией?
2. На какие части условно разбивают импульсный элемент?
3. Каково выражение для импульсной функции формирующего элемента? импульсного фильтра?
4. Как определить передаточную функцию экстраполятора нулевого порядка?
5. Что такое решетчатые функции? С какой целью они используются в описании дискретных систем?
6. Что представляет собой Z-преобразование простое и модифицированное?
7. Как вычислить дискретную передаточную функцию разомкнутой импульсной системы? замкнутой системы?
8. При каком условии дискретная система автоматического управления будет устойчивой?
9. Что представляют собой процессы конечной длительности? Какому условию должен удовлетворять знаменатель передаточной функции замкнутой дискретной САУ для обеспечения процесса конечной длительности?
10. Как составить схему рекуррентного расчета переходного процесса в дискретной САУ на основе ее передаточной функции?
Приложение: М-файл сценарий imp.m
% Программа вычисления параметров импульсной системы, которые отвечают режимам конечной длительности и границе устойчивости
disp('Введите значение величины постоянной времени А1 звена - T1');
T1=input('T1=');
disp('Введите вектор параметров импульсной системы S, используемых для настройки на нужный режим');
disp ('Первые 2 компонента вектора S, отвечают значениям двух из трех ("gamma", "T", "k") параметров, вводимых в заданной последовательности');
disp('третий компонент принимает значение - 1 (ищется "gamma"), - 2 (ищется "T"), - 3 (ищется "k")');
S=input('S=');
% Ниже решаются нелинейные алгебраические уравнения с поиском двух значений настроечного параметра
if S(3)==1
T=S(1); k=S(2);
F1g=@(x)exp(-T/T1)-k*(exp(-(1-x)*T/T1)-exp(-T/T1))+1;Gkr=fzero(F1g,0.5);
F2g=@(x)-exp(-T/T1)+k*(exp(-(1-x)*T/T1)-exp(-T/T1)); Gopt=fzero(F2g,0.5);
disp(['Величина параметра заполнения при настройке на границу устойчивости Gamma_kr=',num2str(Gkr)]);
disp(['Величина параметра заполнения при настройке на режим конечной длительности Gamma_opt=',num2str(Gopt)]);
elseif S(3)==2
gamma=S(1);k=S(2);
F1t=@(x)exp(-x/T1)-k*(exp(-(1-gamma)*x/T1)-exp(-x/T1))+1;Tkr=fzero(F1t,1);
F2t=@(x)-exp(-x/T1)+k*(exp(-(1-gamma)*x/T1)-exp(-x/T1)); Topt=fzero(F2t,1);
disp(['Величина периода квантования при настройке на границу устойчивости T_kr=',num2str(Tkr),'c']);
disp(['Величина периода квантования при настройке на режим кон. длительности T_opt=',num2str(Topt),'c']);
else
gamma=S(1);T=S(2);
F1k=@(x)exp(-T/T1)-x*(exp(-(1-gamma)*T/T1)-exp(-T/T1))+1;Kkr=fzero(F1k,1);
F2k=@(x)-exp(-T/T1)+x*(exp(-(1-gamma)*T/T1)-exp(-T/T1)); Kopt=fzero(F2k,1);
disp(['Величина коэффициента усиления при настройке на границу устойчивости K_kr=',num2str(Kkr)]);
disp(['Величина коэффициента усиления при настройке на режим кон. длительности K_opt=',num2str(Kopt)]);
end
Табл. 4.3. Параметры звеньев импульсной системы
| № п/п | Импульсный элемент | Непрерывная часть системы | ||
| γ | T | T1 | k | |
| ? | 0,8 | 1,75 | 6,5 | |
| 0,15 | 0,5 | 3,5 | ? | |
| 0,352 | ? | 4,5 | 8,5 | |
| 0,2 | 0,5 | 1,75 | ? | |
| ? | 0,85 | 2,5 | 7,5 | |
| 0,3 | 0,75 | 3,25 | ? | |
| 0,5 | ? | 1,25 | 4,5 | |
| 0,8 | 1,1 | 4,0 | ? | |
| 0,35 | ? | 4,5 | 10,5 | |
| ? | 0,25 | 1,0 | 9,5 | |
| ? | 0,62 | 2,5 | 9,5 | |
| 0,5 | 1,0 | 2,0 | ? | |
| 0,75 | 0,6 | 1,0 | ? | |
| ? | 0,77 | 3,5 | 9,5 | |
| 0,3 | 0,8 | 4,0 | ? | |
| 0,7 | ? | 1,0 | 4,5 | |
| ? | 0,96 | 1,5 | 10,0 | |
| 0,5 | ? | 2,0 | 7,5 | |
| ? | 0,83 | 1,25 | ||
| 0,7 | ? | 2,5 | 6,5 | |
| 0,5 | 0,75 | 3,0 | ? | |
| 0,6 | 0,3 | 1,75 | ? | |
| ? | 1,05 | 2,75 | 8,0 | |
| 0,4 | ? | 3,25 | 8,5 | |
| 0,5 | ? |
Дата добавления: 2014-12-23; просмотров: 278; Мы поможем в написании вашей работы!; Нарушение авторских прав |