Теоретическая часть. Система управления называется оптимальной, если для нее обеспечено оптимальное значение некоторого основного показателя J

Система управления называется оптимальной, если для нее обеспечено оптимальное значение некоторого основного показателя J, называемого критерием оптимальности или целевой функцией. Этот критерий обычно зависит от характера протекания переходного процесса и может быть записан в виде:

,

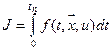где – вектор координат системы, 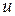– управляющее воздействие.

Поиск алгоритма управления должен производиться с учетом ограничений, наложенных на изменения координат системы и управляющего воздействия. Эти ограничения определяются либо физическими свойствами объекта управления (ОУ), либо задаются при проектировании из условий нормальной работы системы управления. Обычно учитывается, что величина управляющего воздействия на ОУ ограничена, что связано, в свою очередь, с ограничением максимальных ускорений движения ОУ по соображениям механической прочности и безопасности

Важным частным случаем задачи об оптимальном управлении является задача об оптимальном быстродействии систем. Она состоит в нахождении такого алгоритма управления u(t) и такого закона изменения регулируемой величины x(t) (траектории движения ОУ), при котором переход его из произвольного начального состояния в заданное желаемое осуществляется за минимально возможное время (т.е. критерий оптимальности – время процесса). Это означает, что оптимальное управление должно минимизировать функционал:

,

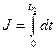при соблюдении ограничения вида 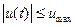. Последнее означает, что условия безопасности эксплуатации ограничивают величину управляющего воздействия, подаваемого на объект.

В ТАУ, на основании принципа максимума Понтрягина Л.С., доказывается, что подобный переход осуществляется с помощью позиционных (кусочно-постоянных) алгоритмов управления. Фельдбаум А.А. доказал, что число интервалов кусочно-постоянного управляющего воздействия (на каждом из которых управляющее воздействие принимает предельное значение) должно быть равно порядку n линейной системы (т.н. теорема об n-интервалах). Это означает, что для систем второго порядка должно быть два интервала постоянства управляющего воздействия и одно переключение между ними, для систем третьего порядка – три интервала постоянства и, соответственно, два переключения и т.д. При этом моменты времени, в которые происходит переключение знака u(t) (переключения релейного элемента), определяются структурой системы, начальными условиями и внешними воздействиями.

Структурная схема системы второго порядка с возможностью оптимизации по быстродействию приведена на рис. 5.1[7]. В системе кроме главной (единичной отрицательной) обратной связи предусмотрена добавочная обратная связь. В нее включено вычислительное устройство ВУ, которое и решает задачу автоматического определения момента времени переключения реле. Определение структуры ВУ, учитывающего все вышеупомянутые факторы, как раз и является задачей синтеза оптимального по быстродействию управления.

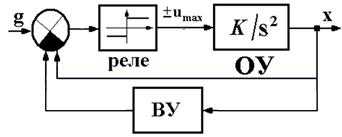Рис. 5.1. Структурная схема САУ 2 порядка оптимальной по быстродействию

Допустим, что, при нулевых начальных условиях, входной сигнал задающего воздействия g(t) изменяется скачкообразно. Тогда при отработке его следует на первом интервале осуществить разгон системы (управляющее воздействие поддерживается на максимальном уровне), а на втором интервале, изменив знак управляющего воздействия, затормозить систему.

В данном случае динамика переходных процессов описывается дифференциальным уравнением второго порядка:

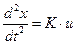, (5.1)

где управляющее воздействие u(t), как уже отмечалось, принимает два возможных предельных значения.

Для расчета структуры ВУ удобно использовать метод фазовой плоскости, для которого задача максимального быстродействия сводится к переводу изображающей точки (ИТ) из произвольного положения в заданное за минимальное время. При этом теорема Фельдбаума определяет, возможность движения ИТ только по фазовым траекториям определенного типа.

Переходя от дифференциального уравнения динамики объекта (5.1) к дифференциальному уравнению фазовой траектории и, интегрируя его, получим выражение вида:

, (5.2)

где С - постоянная интегрирования.

Уравнение (5.2) определяет на фазовой плоскости два семейства фазовых траекторий, соответствующих двум значениям управляющего воздействия и (рис.5.2). Отдельные фазовые траектории каждого из семейств получаются для разных начальных условий, то есть разных значений постоянной интегрирования С в уравнении (5.2).

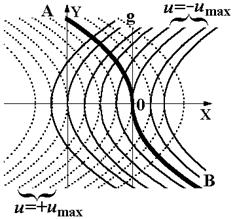
Отработке системой ступенчатого сигнала соответствует переход ИТ из произвольной точки М ( или N) в желаемую точку О (x=g, y=0) (рис.5.2). При этом на первом интервале управления ИТ должна из произвольной точки попасть на линию АОВ, а на втором – должна двигаться по фазовым траекториям, проходящим через эту точку, т.е. по линии АОВ. Именно по достижении ИТ этих отрезков траекторий и должно производиться переключение реле Это условие будет обеспечено, если слева (и снизу) от линии АОВ изобразить фазовые траектории, соответствующие, и справа (и выше) - траектории, соответствующие . Таким образом, управление будет оптимальным по быстродействию, если знак управляющего воздействия изменить в тот момент, когда изображающая точка достигнет линии АОВ.

Поэтому кривую АОВ можно назвать линией переключения. Поскольку участки АО и ОВ линии переключения описываются уравнениями:

,

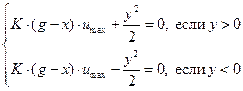то уравнение для всей линии переключения можно записать в виде:

.

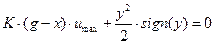Рис. 5.2 Фазовые траектории системы второго порядка оптимальной по быстродействию

Учитывая, что 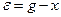, получим окончательно уравнение линии переключения:

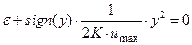. (5.3)

В зависимости от того, лежит ли ИТ выше или ниже линии переключения, знак выражения (5.3) изменяется. Поэтому, для управляющего воздействия можно записать следующее соотношение:

,

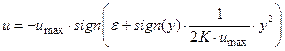или, вводя обозначение 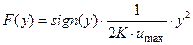, окончательно:

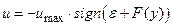. (5.4)

Таким образом, для реализации оптимальной по быстродействию системы ВУ, вычисляющее функцию переключения, должно состоять из дифференциатора и нелинейного преобразователя. Последний, в свою очередь, должен включать в себя квадратор, масштабирующий умножитель сигнала, двухпозиционное реле с единичным уровнем выхода и умножитель.

Фактически ВУ, выдавая сигнал в зависимости от величины скорости изменения выходного сигнала y(t), осуществляет гибкую обратную связь в системе, которая, в отличие от ранее рассмотренных случаев, является нелинейной. Так что структура системы оптимального быстродействия очень близка к структуре обычной двухпозиционной САУ с использованием производных в законе управления (линейной гибкой обратной связью). Принципиальное отличие заключается в том, что весовой коэффициент при производной − T_d :

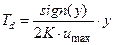
не является постоянной величиной, а уменьшается при приближении ИТ к точке равновесия фазовой плоскости (при уменьшении величины скорости y).

На практике реализация оптимальных по быстродействию систем возможна лишь если можно пренебречь рядом реально существующих факторов:

· возмущениями f;

· запаздыванием передачи сигнала в системе τ;

· отклонениями статической характеристики реального нелинейного элемента от идеальной формы.

Возмущения существенно влияют на конкретный вид особых фазовых траекторий, при этом коррекция линии переключения возможна лишь в том случае, когда возмущения можно точно измерить. Последнее же обстоятельство для реальных технологических объектов весьма проблематично.

Запаздывание ведет к тому, что момент перехода ИТ на новую фазовую траекторию будет отставать от момента переключения на время τ, и ИТ будет двигаться уже не по особой траектории. Естественно, что в этом случае в системе сформируется предельный цикл, , охватывающий начало координат, т.е. возникнут автоколебания.

К аналогичному эффекту приводит наличие у статической характеристики реле петлевой неоднозначности.

Таким образом, оптимальная система с ВУ реализованным согласно вышеописанному алгоритму (5.4), работает устойчиво при больших отклонениях от состояния равновесия, а сама точка равновесия системы, является неустойчивой и вблизи нее формируется устойчивый предельный цикл.

Отметим, что на практике строго оптимальное управление требуется сравнительно редко, важнее получить быстродействие, близкое к предельному значению, но при более простой реализации управляющего устройства. Упрощение сводится к замене нелинейной функции F(y) на линейную функцию, то есть к замене нелинейного преобразователя (НП) линейным звеном с коэффициентом передачи k_gos. Эта ситуация рассматривалась ранее в работе №2 (гибкая обратная связь).

Уравнение линии переключения, полученное в результате такого упрощения, имеет вид:

0=x+k_gos y. (5.5)

Момент начала торможения будет определяться этой прямой переключения, и, как видно из рис. 5.3, оптимальный переходный процесс при данном значении коэффициента гибкой обратной связи будет осуществляться только для одного возможного набора начальных условий (x₀^*=x₀₂ – кривая 2).

Рис. 5.3. Переходные процессы в квазиоптимальной системе с линейным алгоритмом работы ВУ, полученные для различных начальных условий.

Для других начальных значений требуется иной выбор коэффициента передачи k_gos, а для данного значения переходный процесс имеет место либо перерегулирование (кривая 1), либо участок затянутого скользящего режима (кривая 3). В обоих случаях длительность переходного процесса увеличивается и зависит от величины отклонения 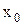от фиксированного значения . Обычно k_gos выбирают из условия, чтобы переходный процесс был оптимальным для некоторого среднего значения 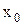из возможного диапазона значений. Получающиеся при таком упрощении системы называются квазиоптимальными.

К квазиоптимальным относят также системы, в которых для подавления автоколебаний, вызванных, например, наличием запаздывания в объекте, производится замена релейного элемента элементом с зоной пропорциональности и последующим насыщением. В правильно настроенных квазиоптимальных системах протекание процессов достаточно близко к оптимальным.