Теоретическая часть. Для нестационарных объектов управления, параметры которых в процессе работы могут меняться непредвиденным образом

Для нестационарных объектов управления, параметры которых в процессе работы могут меняться непредвиденным образом, применение обычных систем управления может не обеспечить требуемого качества управления, а иногда и устойчивости. В силу этого желательно создать такую систему, в которой организовано дополнительное получение информации об изменении динамических свойств объекта в процессе работы и использование этой информации для надлежащего управления. Такая система должна обладать способностью самостоятельно (в реальных условиях при ограниченном участии обслуживающего персонала) оптимизировать свою работу.

Адаптивными САУ (АСАУ) называются системы, которые в процессе выполнения основной задачи управления, автоматически приспосабливаются к изменению свойств ОУ и обеспечивают нужное качество путем изменения параметров (а возможно и структуры) регулятора.

В процессе функционирования АСАУ автоматическая подстройка регулятора производится в зависимости от значения критерия качества или на основе непрерывной идентификации параметров ОУ. В Обычно в адаптивных системах присутствует дополнительный контур адаптации, предназначенный для переработки информации об изменяющихся условиях работы и последующего действия на регулятор основного контура.

Достаточно часто при построении контура адаптации используется метод эталонной модели,которая реализует желаемые динамические характеристики основной системы. Структурная схема системы с эталонной моделью изображена на рис. 6.1

а	б
Рис. 6.1. Организация адаптивных САУ. а – блок-схема АСАУ с эталонной моделью. 1 – нестационарный объект управления, 2 – эталонная модель, 3 –цепь настройки (адаптер и исп. механизм), 4 – перестраиваемый регулятор; верхний замкнутый контур является основным контуром управления, а нижний – контуром адаптации; б – схема системы управления нестационарным объектом первого порядка

Основной задачей синтеза адаптивной системы с эталонной моделью является получение структуры цепи настройки, которое обеспечивает выполнение задачи адаптации. Рассмотрим реализацию этой задачи для простейшего примера системы управления первого порядка. На рис. 6.1б представлена замкнутая схема САР нестационарным объектом первого порядка, при этом для компенсации неконтролируемого изменения положения полюса a(t)[9] коэффициент передачи регулятора k(t) сделан перестраиваемым.

Передаточная функция замкнутой системы имеет вид:

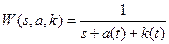. (6.1)

В качестве модели выберем звено с передаточной функцией:

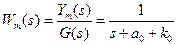, (6.2)

где y_m –выходная координата модели («эталонное» значение регулируемой величины), a₀ , k₀ –жёсткие желаемые значения коэффициентов системы.

Мерой рассогласования выходных сигналов системы и модели является величина отклонения выходного параметра объекта, снабженного адаптивным регулятором, от выходной характеристики эталонной модели . Учитывая изменения знака ε в переходном процессе, выберем в качестве критерия оптимальности квадратичную функцию от величины отклонения .

Сущность работы цепи настройки заключается в организации такого алгоритма перестройки k(t), чтобы в каждый момент времени его изменение 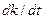было направлено на уменьшение I(k), т.е. требуется выполнение соотношения:

, (6.3)

где параметр λ характеризует степень взаимосвязи этих функций.

Учитывая, что:

,

а также то, что входной и выходной сигналы объекта управления связаны соотношением , то можно записать для величины сигнала производной выражение:

.

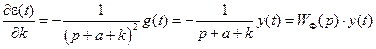Строго говоря, параметры передаточной функции фильтра должны изменяться в соответствии с изменениями параметров системы a(t) и k(t). Однако, поскольку априори эти значения неизвестны, то, в целях упрощения, их можно принять постоянными и равными a₀ и k₀, т.е. соответствующим параметрам эталонной модели:

. (6.4)

В итоге упрощенный алгоритм подстройки коэффициента k имеет следующий вид:

. (6.5)

Для окончательного получения выражения уравнение (6.7) должно быть проинтегрировано по времени, что и выполняется интегратором исполнительного механизма.

Таким образом, в цепь настройки адаптивной системы должны входить (рис. 6.2):

· фильтр, на вход которого подается выходной сигнал системы, − для формирования сигнала ;

· элемент сравнения – для формирования величины рассогласования ε;

· блок умножения − для перемножения этих сигналов;

· исполнительный механизм (интегратор), с коэффициентом передачи λ, для формирования сигнала пропорционального перестраиваемому коэффициенту передачи по обратной связи k(t).

Для реализации в каждый момент времени сигнала по линии обратной связи в нее следует включить блок умножения (см. рис. 6.2).

Эффективность работы адаптивного регулятора будет, вообще говоря, возрастать при увеличении параметра взаимосвязи λ. Однако предел такому повышению ставит имеющийся в канале управления эффект транспортного запаздывания. Поэтому при каждом значении времени транспортного запаздывания τ существует свое оптимальное значение λ^*, для которого эффект адаптации осуществляется наилучшим образом. Это значение и необходимо определить в лабораторной работе.

Рис. 6.2. Структурная схема реализации адаптивной системы с эталонной моделью. Цифрами обозначены элементы, которые идентичны рис. 6.1.