ВЕРОЯТНОСТНУЮ СХЕМУ.

1. Брошены две игральные кости. Какова вероятность того, что на них выпали грани с одинаковым числом очков?

Каждому из шести исходов при броске первой кости соответствует шесть исходов, получающихся при броске второй кости, значит, всего получится 36 элементарных исходов (1-1, 1-2, ..., 1-6, 2 - 1, ... , 6 - 6). Искомому событию благоприятствуют 6 исходов из 36 (1-1, 2-2, ... , 6-6), поэтому вероятность данного события А

.

2. В урне 10 белых и 12 черных шаров, вынимают 3 из них. Какова вероятность того, что среди них ровно 2 черных?

Общее число элементарных исходов - это число способов, которым можно вынуть 3 шара из 22. Оно равно числу сочетаний из 22 элементов по 3.

n =

(первый шар выбирается 22 способами, после того, как первый выбран, второй - 21 способом, а для третьего после выбора первых двух остается 20 вариантов; однако каждый набор из трех шаров мы включили в общее число несколько раз, а именно 3·2·1=6, поэтому разных наборов из 3 шаров в 6 раз меньше, чем 22·21·20).

Общая формула для числа сочетаний из L по k приведена ниже.

Событие А, вероятность которого нужно подсчитать, состоит в том, что вынуты 2 черных и 1 белый шар. 2 черных шара из 12-ти можно извлечь

способами ( 1-й - любой из 12-ти черных, 2-й - любой из 11-ти оставшихся, но каждый набор из двух шаров учтен дважды, поэтому 12·11 делим пополам). 1 белый шар из 10-ти можно взять

способами. Таким образом, число благоприятствующих событию А способов равно

m =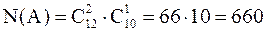

(каждый из 66 наборов из 2 черных шаров и каждый из 10 белых шаров дают устраивающий нас вариант).

Итак,

.

Примечание. Общая формула для числа сочетаний из L по k

,

где .

(подробнее о комбинаторных схемах см. [ 3-4 ]).

3. Полный набор домино (28 костей) раздается между четырьмя игроками (по 7). Какова вероятность, что у третьего игрока нет «шестерок»?

Всего игрок может получить n = различных наборов из 7 костей, составленных из всех 28 костей домино, «шестерка» содержится на 7 «костяшках», значит, без «шестерок» – 21 кость домино. Из них можно составить m = всевозможных «семерок» – наборов из 7 костей. Окончательно,