ВЕРОЯТНОСТЯХ.

Относительная частота события А - это отношение числа испытаний, в которых событие фактически появилось (благоприятствующих А) к общему числу проведенных испытаний: .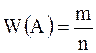

Если классическая вероятность вычисляется до опыта, то относительная частота - после опыта. Конечно, при увеличении количества испытаний в серии на 1 W(A) меняется - хотя бы потому, что на единицу изменяется знаменатель дроби. Тем не менее, с увеличением n величина W(A) приближается к некоторому числу, которое называют статистической вероятностью события А.

Заметим, что когда в задаче говорится, что «вероятность поражения стрелком мишени равна 0,7», то речь идет о вероятности, вычисленной статистически.

Бывают задачи, когда множества всех элементарных исходов и благоприятствующих исходов невозможно пересчитать. В этих задачах иногда удается выразить вероятность события как отношение либо длин, либо площадей, либо объемов. Например, если считать, что попадания в круглую мишень происходят равномерно по площади всей мишени, а диаметр центра мишени в 5 раз меньше диаметра самой мишени, то вероятность попадания в центр (при условии попадания в мишень) равна отношению площадей центра мишени и всей мишени:

В этом случае количество вариантов, благоприятствующих А, бесконечно, но и общее число вариантов исхода испытания бесконечно, т.е. формулы классической или статистической вероятности неприемлемы.

Вероятность, определяемую как отношение длин, площадей, объемов, называют геометрической вероятностью.

§6. ПРОСТЕЙШИЕ СВОЙСТВА ВЕРОЯТНОСТЕЙ.

Для классического, статистического и геометрического определений вероятности выполняются следующие аксиомы:

I. Р(А) ³ 0 для любого наблюдаемого события А ;

II. Р(W ) = 1 ;

III. Если события А и В несовместны (А · В = Æ), то Р(А + В) = Р(А) + Р(В).

Из аксиом можно вывести следующие свойства:

1. Р(Æ) = 0 , откуда следует, что если А и В несовместны (А · В = Æ ), то Р(А · В) = 0.

2. Р( 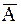) = 1 - Р(А).

3. Р(А) £ 1.

4. Если А Ì В (А влечет за собой В, т.е. все исходы, содержащиеся в А, содержатся и в В), то Р(А) £ Р(В) .

5. Если А = B (т.е. А Ì В и В Ì А), то Р(А) = Р(В) .

6. Р(А + В) = Р(А) + Р(В) - Р(А · В), формула сложения вероятностей. В частности, если А и В несовместны (А · В = Æ), то получим аксиому III.