Методические указания к изучению дисциплины

И выполнению контрольной работы

для студентов заочной формы обучения

Специальности: 080103 - Национальная экономика

080801 - Прикладная информатика в экономике

Санкт-Петербург

Допущено

редакционно-издательским советом СПбГИЭУ

в качестве методического издания

Составители:

доцент В. Г. Блинова

канд. техн. наук, доцент Я. В. Войтишек

ст. преп. Е. Н. Зверева

Рецензент

канд. физ.-мат. наук, доцент Л. Н. Пронин

Подготовлено на кафедре

высшей математики

Одобрено научно-методическими советами специальностей

080103 – Национальная экономика

080801 – Прикладная информатика в экономике

Отпечатано в авторской редакции с оригинал-макета,

представленного составителями

ã СПбГИЭУ, 2007

Содержание

1. Общие положения ………………………………………….. 5

2. Требования к оформлению контрольной работы …………..6

3. Методические указания к изучению дисциплины………… 7

4. Методические указания к выполнению заданий № 1- № 4

Комментарии к задаче № 1

§1. Случайные события. Основные понятия. ………………….7

§2. Случайные события. Операции. ……………………………8

§3. Классическое определение вероятности. …………………..9

§4. Примеры задач на классическую вероятностную схему... 10

§5. О статистической и геометрической вероятностях. ……...12

§6. Простейшие свойства вероятностей. ……………………...13

§7. Условные вероятности. Независимость событий. ………..13

§8. Вероятность наступления хотя бы одного события. ……..14

§9. Формула полной вероятности. …………………………….16

§10. Формула Байеса. …………………………………………..18

Комментарии к задаче № 2

§11. Повторные независимые испытания. ……………………19

§12. Другие формулы вычисления вероятностей для

схемы Бернулли. …………………………………………..22

Комментарии к задаче № 3

§13. Случайные величины дискретного типа. ………………..24

§14. Функция распределения. ………………………………….25

§15. Математическое ожидание случайной

величины дискретного типа. …………………………………..26

§16. Дисперсия случайной величины. ………………………..28

§17. Биномиальный и пуассоновский законы распределения.28

Комментарии к задаче № 4

§18. Случайные величины непрерывного типа. ……………...30

§19. Нормальный закон распределения и его характеристики ………………………………………………... 32

§20. Другие законы распределения непрерывных

случайных величин. …………………………………………33

5. Методические указания к выполнению задания № 5 ……..34

6. Контрольные задания № 1- № 4 …………………………… 55

7. Контрольные задания № 5 …………………………………..73

8. Список литературы ………………………………...………. 82

Приложение 1

Таблица случайных чисел……………..…………………….83

Приложение 2

Нормированная функция Лапласа….……………………….85

Приложение 3

Значение чисел q в зависимости от объёма выборки n и надёжности для определения доверительного интервала среднего квадратического отклонения 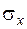…………………87

Приложение 4

Критические точки распределения …………………..….88