
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Виды средних величин
Из всего многообразия средних величин наиболее часто в экономической статистике применяются: средняя агрегатная, средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя хронологическая. Применение той или иной формы зависит от содержания осредняемого признака и конкретных данных, по которым ее необходимо рассчитать.
1. Средняя агрегатная вычисляется по формуле:
 , (21)
, (21)
где wi – объемный показатель;
fi – вес признака, частота, численность.
Формула агрегатной средней используется, если известны значения числителя и знаменателя в логической формуле (СИС).
Если известны фонд оплаты труда (ФОТ) и численность в отдельных цехах (участках), то средняя заработная плата по предприятию определяется по формуле (табл. 8):
 , (22)
, (22)
Таблица 8
Фонд оплаты труда ООО «Вымпел»
| № цеха | ФОТ, тыс. руб. | Численность, чел. |

2.Средняя арифметическая и ее свойства.Средняя арифметическая – одна из наиболее распространенных форм средней величины. Средняя арифметическая используется, если даны отдельные значения признака или в логической формуле расчета показателя неизвестен числитель. Она применяется в виде простой и взвешенной средней арифметической.
Формула простой:
 , (23)
, (23)
где xi – отдельные значения признака;
n – число единиц совокупности, число значений признака.
Часто в совокупности отдельные варианты могут принимать одинаковые значения, которые можно объединить в группы, подсчитав их численность, поэтому в этом случае осуществляется переход к средней взвешенной. Ее можно определить как частное от деления суммы произведения вариантов и их численностей (частот) – Sx × f на сумму численностей (частот) – Sf.
 , (24)
, (24)
где xi – отдельные значения признака, значения вариантов (показателей);
fi – численность (частота, вес) каждого варианта (группы).
Основой для вычисления простой арифметической служат первичные записи результатов наблюдения, а для взвешенной – обработанный материал, сгруппированные данные по количественному признаку.
Простая средняя вычисляется в тех случаях, когда веса отсутствуют, или их очень трудно определить, или если численность отдельных групп (вариантов) не слишком отличается. В других случаях ее применение приводит к очень грубым ошибкам. Простая средняя соответствует простой совокупности объектов, в которой нет групп.
Средняя взвешенная отражает сложное строение совокупности, в ней учитывается удельный вес отдельных групп в совокупности.
Средняя арифметическая имеет ряд свойств, которые находят практическое применение:
1-е свойство. От увеличения (уменьшения) всех вариантов осредняемой величины в К раз их средняя величина соответственно увеличивается (уменьшается) в К раз.
Zi = K × Хi
 (25)
(25)
2-е свойство. От уменьшения (увеличения) веса каждого варианта в К раз средняя не меняется.
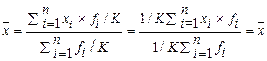 (26)
(26)
3-е свойство. Величина средней зависит не от абсолютных значений весов отдельных вариантов, а от пропорций между ними.
Отношения отдельных частот f1, f2, … fn к Σfi представляют долю отдельных вариантов в совокупности:
 (27)
(27)
где di – удельный вес, часть, доля.
Поэтому вместо абсолютного значения fi можно брать веса вариантов, выраженные в долях или процентах, тогда
 (28)
(28)
4-е свойство. Если уменьшить (увеличить) все варианты осредненного признака на постоянное число (А), то средняя уменьшается (увеличивается) на то же число.
Zi = xi – А
 (29)
(29)
5-е свойство. Средняя, умноженная на численность всей совокупности, равна сумме произведения каждого варианта на ее численность.
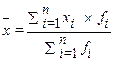
 ×
×  fi =
fi =  хi × fi (30)
хi × fi (30)
6-е свойство. Сумма отклонений индивидуальных значений от их средней арифметической равна нулю.
 (хi –
(хi –  ) × fi = 0,
) × fi = 0,
 хi × fi –
хi × fi –  ×
×  fi = 0, (31)
fi = 0, (31)
так как  xi × fi =
xi × fi =  ×
×  fi (свойство 5).
fi (свойство 5).
То есть если взять отклонения каждого варианта от средней величины и взвесить по численности, а затем сложить, то получим ноль.
7-е свойство. Сумма квадратов отклонений индивидуальных значений от их средней арифметической меньше, чем сумма квадратов отклонений индивидуальных значений от любой другой величины:
 (хi –
(хi –  )2 <
)2 <  (хi – А)2. (32)
(хi – А)2. (32)
Использование свойств средней арифметической позволяет значительно упростить ее вычисления. Упрощенный способ расчета средней арифметической, называемый способом моментов (первого порядка), состоит в следующем:
– уменьшим все значения вариантов на величину А, в качестве которой обычно принимается наиболее часто встречающееся значение признака: хi – А;
– все полученные отклонения разделим на какое-нибудь общее кратное (обычно величину интервала) число, то же и для весов, то есть

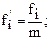 (33)
(33)
– рассчитаем среднюю арифметическую условных значений (Zi):
 (34)
(34)
fi´ = fi / m;
– на основании свойств средней арифметической, для того чтобы ее общее значение не изменялось, нужно условную среднюю Z увеличить в К раз и на А, то есть
 =
=  × К + А. (35)
× К + А. (35)
3.Средняя гармоническаяиспользуется в тех случаях, когда известны обратные значения показателя либо в логической формуле расчета показателя неизвестен знаменатель. Средняя гармоническая вычисляется из обратных значений признака и может также быть:
а) простой
 (36)
(36)
где 1/хi – обратные значения вариантов признака;
n – число вариантов;
б) взвешенной
 (37)
(37)
где wi = хi × fi – объемный показатель.
Применяется средняя гармоническая в тех случаях, когда непосредственные данные о весах отсутствуют, а известны варианты осредняемого признака (хi) и произведения значений вариантов на количество единиц, обладающих данным его значением (wi = хi × fi).
Пример. Рассчитаем среднюю гармоническую величину по данным о валовом сборе зерна, представленным в табл. 9.
Таблица 9
Валовой сбор зерна
| Показатель | Валовой сбор (ВС) | Урожайность (ц/га) – х |
| 1-й участок | ||
| 2-й участок | ||
| 3-й участок |

где площадь определяется как:

Подставляем в исходную формулу:
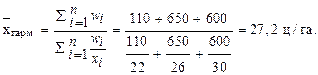
4. Средняя геометрическаяиспользуется в статистике в основном для вычисления темпов роста показателей динамического ряда. В зависимости от имеющихся исходных данных может использоваться формула двух видов:
1. Если расчет ведется исходя из коэффициентов (темпов) роста, найденных по отношению к предыдущему периоду (цепных), то
 (38)
(38)
где Трi – цепные темпы роста;
n – число значений признака.
2. Если в распоряжении имеются абсолютные уровни ряда или базисный темп роста, то есть за весь период, то
 (39)
(39)
где Yо, Yn – начальные и конечные абсолютные значения уровней ряда;
Трбаз – базисный темп роста за данный период.
Например, в 2009 г. валовой продукт (ВП) составил 120 млрд. руб.; в 2004 г. ВП – 100 млрд. руб.

5. Средняя хронологическаяиспользуется для вычисления средней величины из уровней моментного ряда динамики и может быть:
а) простой
 (40)
(40)
где хi – абсолютные значения уровней для моментного ряда (на определенную дату, момент);
(n – 1) – продолжительность периода (например, если за год, то n – 1 = 12 месяцев);
б) взвешенной
 (41)
(41)
где ti – период времени, отделяющий один уровень ряда от другого.
Средняя взвешенная используется, если интервалы времени между уровнями неравны и известно время, в течение которого сохранялось каждое значение уровня ряда.
Дата добавления: 2014-12-23; просмотров: 1047; Мы поможем в написании вашей работы!; Нарушение авторских прав |