Взвешенная

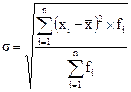(50)

или

где – средняя величина квадрата значений признака (то есть средняя из квадратов);

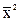– квадрат средней величины признака.

При его определении принимаются в расчет все отклонения значений признака (так как поэтому возводят в квадрат).

Между средним абсолютным и средним квадратическим отклонением существует следующее примерное соотношение: σ ≈ 1,25d (если фактическое распределение близко к нормальному). Чем меньше величина среднего квадратического отклонения, тем однороднее совокупность.

Дисперсия (σ²) вычисляется для всей статистической совокупности в целом как средний квадрат отклонений значения признака от общей средней, измеряет степень колеблемости признака, его вариацию, порождаемую всей совокупностью действующих на него факторов, и определяется по формулам:

простая

(51)

взвешенная:

(52)

.

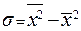Дисперсия имеет ряд свойств, которые находят практическое применение:

1-е свойство. Уменьшение (увеличение) всех значений признака на одну и ту же величину (А) не меняет величины σ² (так как разность между «новым» значением признака и «новой» средней остается без изменения).

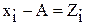, тогда . (53)

Отсюда

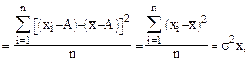
то есть

.

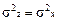2-е свойство. Уменьшение (увеличение) всех значений признака в К раз уменьшает (увеличивает) дисперсию в К² раз.

тогда

. (54)

Согласно свойству средней

,

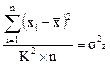то есть

σ²_х = К² × σ²_z.

На основании данных свойств разрабатывается упрощенный метод вычисления дисперсии с помощью способа моментов (2-го порядка):

а) исходные значения вариант признака Хi заменяют условными

, (55)

где А – обычно значение признака, которое чаще всего встречается в совокупности,

К – величина интервала, кратное число;

б) определяется дисперсия условной величины (Z):

(56)

в) определяется дисперсия исходного признака:

(57)

Правило сложений дисперсий.

Общая дисперсия измеряет вариацию результативного признака по всей совокупности под влиянием всех факторов, обусловивших эту вариации.

Межгрупповая дисперсия характеризует систематическую вариацию под воздействием признака – фактора, положенного в основание группировки. Она равны среднему квадрату отклонений групповых (частных) средних от общей средней для всей совокупности:

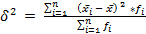, (58)

Внутригрупповая дисперсия применяется к отдельной группе и обозначается как и общая дисперсия (σ²), но с индексом i, который подчеркивает, что расчет выполняется для отдельной i-ой группы.

Внутри групповая дисперсия отражает случайную вариацию, то есть ту ее часть, которая обусловлена влиянием прочих (неучтенных) факторов, отличных от основания группировки.

Существует формула, связывающая общую дисперсию, межгрупповую дисперсию и среднюю по внутригрупповым дисперсиям

, (59)

Это означает. что общая дисперсия равна сумме межгрупповой дисперсии и средней по внутригрупповым дисперсиям.

Правило сложения дисперсий показывает, что чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака на изучаемый результативный признак.

Относительные показатели вариации - являются относительной мерой вариации и представляют собой отношение именованного показателя вариации (R, d, σ) и средней величины ( 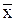, Мо или Ме). Таким образом, в принципе возможен расчет девяти коэффициентов вариации. Они дают представление о степени однородности совокупности. Чем меньше их величины, тем меньше варианты признака отличаются один от другого по величине, тем, следовательно, однороднее совокупность. Будучи относительной величиной, абстрагируют различия абсолютных величин вариации различных признаков и дают возможность сравнения. То есть с их помощью можно сравнивать размеры вариации одного признака в нескольких совокупностях. Чаще на практике используются следующие:

а) коэффициент осцилляции:

, (60)

б) относительное линейное отклонение

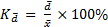, (61)

в) коэффициент вариации

, (62)

При этом из них чаще всего используется коэффициент вариации (V).

Коэффициент вариации используют не только для сравнительной оценки вариации, но для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений близких к нормальному).