
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вариация признака в совокупности
Составной частью сводной обработки данных статистического наблюдения является построение рядов распределения. Рядом распределения называется группировка, в которой для характеристики групп (упорядоченно расположенных по значению признака) применяется один показатель – численность группы. Цель построения ряда – выявление основных свойств и закономерностей исследуемой статистической совокупности.
В зависимости от того, является ли признак, взятый за основу группировки, качественным или количественным, различают соответственно два типа рядов распределения – атрибутивные и вариационные.
По характеру вариации различают дискретные и непрерывные признаки. Дискретные признаки отличаются друг от друга на некоторую конечную величину; непрерывные могут отличаться один от другого на сколь угодно малую величину и в определенных границах принимать любые значения.
Первый шаг в упорядочении первичного ряда – его ранжирование, то есть расположение всех вариантов ряда в возрастающем или убывающем порядке.
Число повторений отдельных вариантов значений признаков называют частотой повторения. Частота повторения обозначается fi; сумма частот, равная объему изучаемой совокупности, – 
Частоты, представленные в относительном выражении, называются частостями:  .
.
Частости могут быть выражены в долях единицы или в процентах.
Например, распределение рабочих участка по квалификации и их характеристика представлены в табл. 11.
Таблица 11
Квалификационные характеристики рабочих участка «С»
| Тарифный разряд рабочего xi | Число рабочих, имеющих этот разряд, fi | Частость wi | Накопленная частота Si |
| 0,05 | |||
| 0,025 | |||
| 0,40 | |||
| 0,20 | |||
| 0,10 | |||
| Итого | 1,00 |
В тех случаях, когда число вариантов дискретного признака достаточно велико, а также при анализе вариации дискретного признака, когда значение признака у отдельных единиц может вообще не повторяться, строятся интервальные ряды распределения.
Для определения величины интервала h для построения вариационного ряда с равными интервалами:
1) вычисляется разность между максимальным и минимальным значениями признака первичного ряда (размах вариации – R):
 (63)
(63)
2) размах вариации делится на число групп k, то есть 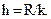 Число групп приближенно определяется по формуле Стэрджесса: k ≈ 1 + 3,322 · lgN, где N – общее число изучаемых единиц совокупности. Полученная величина округляется до целого числа.
Число групп приближенно определяется по формуле Стэрджесса: k ≈ 1 + 3,322 · lgN, где N – общее число изучаемых единиц совокупности. Полученная величина округляется до целого числа.
Рассмотрим пример построения ряда распределения по первичным данным о размере прибыли 20 коммерческих банков за год (млн. руб.):
 .
.
Количество групп равно: k ≈ 1 + 3,322 · lgn20 = 5,32.
Округляя, получаем число групп, равное 5.
Величина интервала (h) определяется: 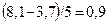 млн. руб.
млн. руб.
В результате группировки получаем ряд распределения (табл. 12).
Таблица 12
Распределение банков по величине прибыли
| Размер прибыли, млн. руб. | Число банков | Накопленная частота |
| 3,7-4,6 | ||
| 4,6-5,5 | ||
| 5,5-6,4 | ||
| 6,4-7,3 | ||
| 7,3-8,1 | ||
| Итого |
Знак «–» в первой строке соответствует принципу «исключительно» и означает, что значения признака, совпадающие с верхней границей интервала, в этот интервал не включаются, а попадают в следующий интервал. Если ставится знак «+», это соответствует принципу «включительно» и означает, что значения признака, совпадающие с верхней границей интервала, включаются в эту группу.
Дата добавления: 2014-12-23; просмотров: 1158; Мы поможем в написании вашей работы!; Нарушение авторских прав |