
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Показатели центра распределения
Для характеристики среднего значения признака в вариационном ряду используются средняя арифметическая величина, медиана и мода. Рассмотрим расчет показателей центра распределения для вариационных рядов.
Средняя арифметическая:
– для дискретного ряда распределения
 , (64)
, (64)
где xi – вариант значений;
fi – частота повторения данного варианта;
– для интервального ряда распределения
 , (65)
, (65)
где  – средняя соответствующего интервала.
– средняя соответствующего интервала.
Для табл. 11 средняя арифметическая равна:
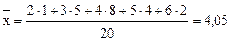 .
.
Для табл. 12 средняя арифметическая равна:
 млрд. руб.
млрд. руб.
Медиана:
– для дискретного ряда распределения положение медианы определяется ее номером  , где n – число единиц совокупности.
, где n – число единиц совокупности.
Для примера в табл. 11  , то есть медиана равна средней арифметической 10-го и 11-го значений признака. Ме = 4;
, то есть медиана равна средней арифметической 10-го и 11-го значений признака. Ме = 4;
– для интервального ряда распределения сразу можно определить интервал, в котором находится медиана. Затем определяем медиану по формуле:
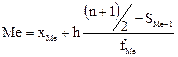 , (66)
, (66)
где хМе – нижняя граница медианного интервала;
h – величина интервала;
SMe-1 – накопленная частота интервала, предшествующая медианному;
fMe – частота медианного интервала.
Для примера, приведенного в табл. 12,
 млрд. руб.
млрд. руб.
Мода:
– для дискретного ряда распределения – наиболее часто встречающееся значение. Для табл. 11 мода равна 4 (максимальная частота 8);
– для интервального ряда распределения
 , (67)
, (67)
где xMo – нижняя граница модального интервала;
fMo – частота, соответствующая модальному интервалу;
fMo-1 – предмодальная частота;
fMo+1 – послемодальная частота.
Для примера, приведенного в табл. 12,
 млрд. руб.
млрд. руб.
Дата добавления: 2014-12-23; просмотров: 276; Мы поможем в написании вашей работы!; Нарушение авторских прав |