Показатели формы распределения

Для получения приблизительного представления о форме распределения строят графики распределения (полигон и гистограмму). Эмпирическое распределение строится на основе выборки из исследуемой генеральной совокупности. Поэтому эмпирические данные в определенной степени связаны со случайными ошибками наблюдения. Кривая теоретического распределения показывает распределение, которое получилось бы при полном погашении всех случайных причин, затемняющих основную закономерность.

Выяснение общего характера распределения предполагает оценку степени его однородности, а также вычисление показателей асимметрии и эксцесса.

Симметричным является распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой. Для сравнительного анализа степени асимметрии рассчитывают относительный показатель As:

. (68)

Другой показатель асимметрии, предложенный Линдбергом,

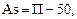(69)

где П – процент тех значений признака, которые превосходят по величине среднюю арифметическую.

Наиболее точным и распространенным является показатель, рассчитываемый следующим образом:

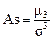, где . (70)

Положительная величина указывает на наличие правосторонней асимметрии (в этом случае ). Отрицательный знак свидетельствует о наличии левосторонней асимметрии ( ).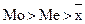

Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. Показатель эксцесса, предложенный Линдбергом

Ех = П – 38,29, (72)

где П – доля (%) количества вариантов, лежащих в интервале, равном половине среднего квадратического отклонения в ту и другую сторону от средней арифметической.

Наиболее точным является показатель, рассчитываемый по формуле:

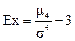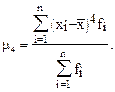, где (73)

Значения эксцесса могут быть положительными (для островершинных распределений) и отрицательными (для плосковершинных).