Средние показатели ряда динамики. Статистические показатели, рассчитанные по уровням ряда динамики, изменяются во времени, варьируют по годам

Статистические показатели, рассчитанные по уровням ряда динамики, изменяются во времени, варьируют по годам. Это требует их обобщения и расчета средних показателей, которые характеризуют общее развитие явления за данный период. К таким обобщающим характеристикам динамического ряда относят:

1) средний уровень ряда ( );

2) средний абсолютный прирост (D );

3) средний темп роста ( );

4) средний темп прироста ( ).

1.Средний уровень ряда – временная или хронологическая средняя – рассчитывается как средняя величина из уровней ряда. Вычисляется по-разному для интервальных и моментных рядов.

Чтобы найти средний уровень (среднюю величину показателя) интервального ряда, достаточно сумму уровней ряда разделить на число периодов, к которым они относятся:

, (132)

где n+1 – число уровней ряда.

Используя данные табл. 13, получим:

Средний уровень моментного ряда рассчитывается на основе средней хронологической:

, (132)

Например, n показывает период, за который определяется вид средней величины: так, средняя за квартал n = 3 месяца, за год n = 12 месяцев. Следовательно, для расчета среднего уровня за квартал нужно иметь 4 значения, за год – 13.

Для неполных моментных рядов применяется взвешивание суммы каждой смежной пары уровней по продолжительности периода между ними, то есть средняя хронологическая взвешенная:

(133)

где ti – время между моментом регистрации y₁ и y₂, y₂ и y₃ и т.п.

2.Средний абсолютный прирост есть средняя из абсолютных приростов за промежутки времени данного периода.

(134)

где n – число абсолютных приростов (тогда уровней соответственно n + 1), то есть

Средний абсолютный прирост показывает, на сколько абсолютных единиц в среднем за период изменяются уровни ряда. Может быть со знаком «+» – прирост или «–» – снижение.

Используя данные табл. 16, получим

=1 кг/год

(четыре уровня и три абсолютных прироста).

= 4,25 кг/год

(пять уровней и четыре абсолютных прироста).

3. Средний темп роста( ) является обобщающим показателем темпов роста уровней ряда динамики и показывает, как в среднем изменялись уровни ряда динамики на протяжении исследуемого периода. Для его расчета всегда используется формула средней геометрической:

– если имеются данные об абсолютных уровнях ряда или базисные темпы роста, то

(135)

где y_n, y₀ – конечный и начальный уровни ряда;

n – число приростов;

Тр_баз – темп роста базисный за весь период.

Для данных из табл. 16

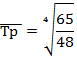
(за четыре года)

– если имеются данные о цепных коэффициентах роста, то

где Т_1,2,..,n – цепные коэффициенты роста;

n – число цепных коэффициентов роста.

4. Средний темп прироста ( ) показывает, на сколько процентов в среднем изменяются уровни ряда за данный период, вычисляется только исходя из средних темпов роста, для чего пользуются соотношением:

или

(136)

Следовательно, для вычисления среднего темпа прироста вначале нужно обязательно определить средний темп роста, а затем уже средний темп прироста.

Применение перечисленных показателей динамики является первым этапом анализа ряда динамики, позволяющим выявить скорость, интенсивность развития явления, представленного рядом.