Аналитическое выравнивание ряда

Определение тренда (аналитического выражения) является наиболее эффективным способом выявления основной тенденции развития явления.

При этом уровни ряда динамики выражаются в виде функции времени:

y_t = f (t).

Аналитическое выравнивание состоит в подборе для данного ряда динамики теоретической кривой, выражающей основные черты фактической динамики, то есть в подборе теоретической кривой, наилучшим образом описывающей эмпирические (фактические) данные.

Аналитическое выравнивание может проводиться с использованием различных трендов.

1. Наиболее простым является выравнивание по прямой:

y_t = a₀ + a₁ × t, (137)

где t – условное обозначение времени;

a₀, a₁ – параметры искомой прямой.

Параметры прямой, удовлетворяющие методу наименьших квадратов, находятся из решения системы уравнений:

(138)

где y – фактические значения уровней;

n – число уровней ряда.

Систему уравнений можно упростить, если t подобрать так, чтобы сумма была равна 0, то есть начало отсчета времени перенести в середину рассматриваемого периода, тогда

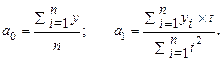(139)

При этом подбор t осуществляется:

а) если число уровней ряда четное, то условное обозначение времени t строится следующим образом: …-7-5-3-1+1+3+5+7… (то есть два серединных момента принимаются –1, +1. Все остальные, соответственно, обозначаются через 2 интервала);

б) при нечетном числе отсчет ведется от середины, принятой за ноль, через единицу: …-3-2-1 0+1+2+3…

Значения можно находить, пользуясь следующими формулами:

(140)

(n – четное)

(141)

(n – нечетное)

2. Выравнивание по параболе (2-го порядка). Если выравнивание производить по многочлену более высокой степени (например, 2-го порядка): yt = a₀ + a₁t + a₂t², то система нормальных уравнений, получаемых методом наименьших квадратов, для определения параметров параболы имеет вид:

na₀ + a₁ t + a₂ t² = y_i;

a₀ t + a₁ t² + a₂ t³ = y_it; (142)

a₀ t² + a t³ + a t⁴ = y_it².

Для упрощения системы t подбираем так, чтобы t = 0 и t³ = 0 (как показано ранее), тогда система упростится:

na₀ + a₂ t² = y_i;

a₁ t² = y_it;

a₀t² + a₂ t⁴ = y_it²,

следовательно,

(143)

где a₀, a₂ определяются решением системы из 2 уравнений;

a₀ – величина, выражающая средние условия образования уровней ряда;

a₁ – скорость развития;

a₂ – ускорение этого развития.

Аналитическое выравнивание можно проводить и по многочленам более высоких степеней, например, параболе 3-го порядка:

yt = a₀ + a₁t + a₂t² + a₃t³. (144)

3. Показательная функция применительно к выравниванию имеет следующий вид:

yt = a₀ × a₁^t , (145)

где a₀ – начальный уровень ряда;

a₁ – среднегодовой темп роста.

Для определения параметров уравнения методом наименьших квадратов, предварительно логарифмируют уровни, тогда логарифмы уровней отражаются линейной функцией:

lgyt = lga₀ + t × lga₁; (146)

если t = 0, то

lga₁ = t × lgy / t².

При этом, чем выше порядок параболы, тем более точно она воспроизводит фактические данные.

Однако основной целью построения аналитического уравнения является не просто воспроизведение фактических данных, а определение тенденции развития данного явления во времени. Основанием для выбора формы кривой для выравнивания служит анализ сущности явления.