Множественная линейная регрессия

Парная корреляция или парная регрессия могут рассматриваться как частный случай отражения связи некоторой зависимости переменной, с одной стороны, и одной из множества независимых переменных – с другой. Когда же требуется охарактеризовать связь всего указанного множества независимых переменных с результативным признаком, говорят о множественной корреляции или множественной регрессии.

Рассмотрим вопрос о регрессии. В ряде случаев именно от его решения – оценки уравнения регрессии – зависят оценки тесноты связи, а они, в свою очередь, дополняют результаты регрессивного анализа. Прежде всего следует определить перечень независимых переменных Х, включаемых в уравнение. Это должно делаться на основе теоретических положений. Список Х может быть достаточно широк и ограничен только исходной информацией. На практике теоретические положения о сути взаимосвязи подкрепляются парными коэффициентами корреляции между зависимой и независимыми переменными. Отбор наиболее значимых из них можно провести с помощью ЭВМ, выбирая в соответствии с коэффициентами корреляции и другими критериями факторы, наиболее тесно связанные с Y. Параллельно решается вопрос о форме уравнения. Современные средства вычислительной техники позволяют за относительно короткое время рассчитать достаточно много вариантов уравнений. В ЭВМ вводятся значения зависимой переменной Y и матрица независимых переменных Х, принимается форма уравнения, например линейная. Ставится задача включить в уравнение k наиболее значимых Х. В результате получим уравнение регрессии с k наиболее значимыми факторами. Аналогично можно выбрать наилучшую форму связи. Этот традиционный прием, называемый пошаговой регрессией, если он не противоречит качественным посылкам, достигает приемлемых результатов. Первоначально обычно берется линейная модель множественной регрессии:

(154)

или в форме уравнения регрессии –

Y_ТЕОР = a₀ + a₁X₁ + a₂X₂ +…+ a_kX_k,

где Y_теор – расчетное значение регрессии, которое представляет собой оценку ожидаемого значения Y при фиксированных значениях Х₁, Х₂, …, Х_k;

а₁, а₂, …, а_k – коэффициенты регрессии, каждый из которых показывает, на сколько единиц изменится Y с изменением соответствующего признака X на единицу при условии, что остальные признаки останутся на прежнем уровне.

Параметры уравнения множественной регрессии, как правило, находятся методом наименьших квадратов. В матричной записи система уравнений имеет вид:

,

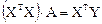где

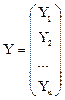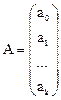; ; . (155)

Оценка параметров множественной регрессии вручную затруднительна, приводит к потерям точности и может лишь удовлетворить любопытство. Получение же оценок параметров на ЭВМ в настоящее время не представляет большой проблемы. Гораздо важнее, насколько линейная форма связи соответствует реально существующей зависимости между Y, с одной стороны, и множеством Х, с другой.