Линейная регрессия

Простейшим приемом выявления связи между двумя признаками является построение корреляционной таблицы(см. табл. 19).

В основу группировки положены два изучаемых во взаимосвязи признака – Х и Y. Частоты f_ij показывают количество соответствующих сочетаний Х и Y. Если f_ij расположены в таблице беспорядочно, можно говорить об отсутствии связи между переменными. В случае образования какого-либо характерного сочетания f_ij допустимо утверждать о связи между X и Y. При этом, если f_ij концентрируются около одной из двух диагоналей, имеет место прямая или обратная линейная связь.

Таблица 19

Пример корреляционной таблицы

Y X	Y1	Y2	…	Yz	Итого
	f11		…	f1z
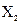
	f21		…	f2z
…	…	…	…	…	…	…
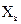
	fk1	k2	…	fkz
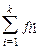
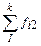
Итого			…		n
			…			–

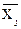
Наглядным изображением корреляционной таблицы служит корреляционное поле. Оно представляет собой график, где на оси абсцисс откладывается значение Х, на оси ординат – Y, а точками показывается сочетание X и Y. По расположению точек, их концентрации в определенном направлении можно судить о наличии связи. В итогах корреляционной таблицы по строкам и столбцам приводятся два распределения – одно по Х, другое по Y. Рассчитываем для каждого X_i среднее значение Y, то есть , как:

, (147)

.

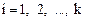Последовательность точек (Х_i, ) дает график, который иллюстрирует зависимость среднего значения результативного признака Y от факторного X, – эмпирическую линию регрессии, наглядно показывающую, как изменяется Y по мере Х.

По существу, и корреляционная таблица, и корреляционное поле, и эмпирическая линия регрессии предварительно уже характеризуют взаимосвязь, когда выбраны факторный и результативный признаки и требуется сформировать предложения о форме и направленности связи. В то же время количественная оценка тесноты связи требует дополнительных расчетов.

Практически для количественной оценки тесноты связи широко используют линейный коэффициент корреляции. Иногда его называют просто коэффициентом корреляции. Если заданы значения переменных X и Y, то он вычисляется по формуле:

. (148)

Можно использовать и другие формулы, но результат должен быть одинаковым для всех вариантов расчета.

Коэффициент корреляции принимает значение в интервале от –1 до +1. Принято считать, что если |r| < 0,30, то связь слабая; при |r| = (0,3/0,7) – средняя; при |r| = > 0,70 – сильная, или тесная. Когда |r| = 1 – связь функциональная. Если же r ≈ 0, то это дает основание говорить об отсутствии линейной связи между Y и X. Однако в этом случае возможно нелинейное взаимодействие, что требует дополнительной проверки и других измерителей, рассматриваемых ниже.

Для характеристики влияния изменений Х на вариацию Y служат методы регрессионного анализа. В случае парной линейной зависимости строится регрессионная модель

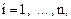(149)

где n – число наблюдений;

а₀, а₁ – неизвестный параметр уравнения;

ε_i – ошибка случайной переменной Y.

Уравнение регрессии записывается как:

Y_iТЕОР = a₀ + a₁X_i, (150)

где Y_iТЕОР – рассчитанное значение результативного признака после подстановки в уравнение Х.

Параметры а₀ и а₁ оцениваются с помощью процедур, наибольшее распространение из которых получил метод наименьших квадратов. Его суть заключается в том, что наилучшие оценки а₀ и а₁ получают, когда

(151)

То есть сумма квадратов отклонений эмпирических значений зависимой переменной от вычисленных по уравнению регрессии должна быть минимальной. Сумма квадратов отклонений является функцией параметров а₀ и а₁. Ее минимизация осуществляется решением системы уравнений:

(152)

Можно воспользоваться и другими формулами, вытекающими из метода наименьших квадратов, например:

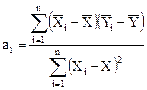или , (153)

.

Аппарат линейной регрессии достаточно хорошо разработан и, как правило, имеется в наборе стандартных программ оценки взаимосвязи для ЭВМ. Важен смысл параметров: а₁ – это коэффициент регрессии, характеризующий влияние, которое оказывает изменение Х на Y. Он показывает, на сколько единиц в среднем изменится Y при Х на одну единицу. Если а₁ больше 0, то наблюдается положительная связь. Если а₁ имеет отрицательное значение, то увеличение Х на единицу влечет за собой уменьшение Y в среднем на а₁. Параметр а₁ обладает размерностью отношения Y к X.

Параметр а₀ – это постоянная величина в уравнении регрессии. На наш взгляд, экономического смысла он не имеет, но в ряде случаев его интерпретируют как начальное значение Y.

Например, по данным о стоимости оборудования Х и производительности труда Y методом наименьших квадратов получено уравнение:

.

Коэффициент «а₁» означает, что увеличение стоимости оборудования на 1 млн. руб. ведет в среднем к росту производительности труда на 2,08 тыс. руб.

Значение функции Y = a₀ + a₁X называется расчетным значением и на графике образует теоретическую линию регрессии.

Смысл теоретической регрессии состоит в том, что это оценка среднего значения переменной Y для заданного значения Х.