
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интерполяция и экстраполяция
Выравнивание рядов динамики используют не только для выявления тенденций, но и для того, чтобы найти недостающее значение уровня ряда. Такой способ нахождения недостающего значения внутри рассматриваемого периода, основанный на выравнивании рядов динамики, называется интерполяцией. Другой прием заключается в том, что мы, продолжая данные математические кривые, тем самым как бы предсказываем дальнейшее развитие явления, то есть на основе выявления особенностей изменения явлений за данный период пытаемся предугадать поведение явления в будущем (прошлом). Он называется экстраполяцией.
Экстраполяцию и интерполяцию можно осуществить различными способами. Но они обязательно основываются на предположении о том, что закономерность (тенденция) изменения изучаемого явления, выявленная для определенного периода времени, сохранится на ограниченном отрезке времени как в будущем (прошлом), так и внутри данного периода.
 Так как в действительности тенденция может измениться, то полученные таким путем данные надо рассматривать как своего рода оценку. Рассмотрим некоторые простейшие приемы, помогающие прогнозировать те или иные показатели за определенный отрезок времени.
Так как в действительности тенденция может измениться, то полученные таким путем данные надо рассматривать как своего рода оценку. Рассмотрим некоторые простейшие приемы, помогающие прогнозировать те или иные показатели за определенный отрезок времени.
1. Прогнозирование на основе среднего абсолютного прироста.Если при анализе ряда динамики обнаруживается, что абсолютные приросты уровней примерно постоянны, то в этом случае рассчитывают средний абсолютный прирост и последовательно прибавляют (вычитают) его к последнему известному уровню ряда столько раз, на сколько периодов экстраполируют (интерполируют) ряд.
Разберем это на основе данных, представленных в табл. 17.
Таблица 17
Производство обуви ОАО «Вест»
| Показатель | 2005 г. | 2006 г. | 2007 г. | 2008 г. |
| Производство обуви, тыс. пар | ||||
| Dyi = yi – yi –1 | – | +13 | +8 | +11 |

Определим объем производства 2010 г.:
y26 = 820 + 10,7 × 2 = 841,4 тыс. пар.
Аналогично можно и интерполировать: на основе среднего абсолютного прироста и последнего перед недостающим уровнем значения ряда:
y2007 = у2008 – 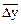 × n = 820 – 10,7 = 809,3 тыс. пар,
× n = 820 – 10,7 = 809,3 тыс. пар,
то есть оценку, а не точные значения дает прогнозирование.
2. Прогнозирование на основе среднегодового темпа роста. Если за исследуемый ряд лет годовые коэффициенты роста относительно постоянны, то в этом случае можно рассчитать средний коэффициент роста и последний известный уровень ряда умножить (разделить) на средний коэффициент роста в степени, соответствующей периоду экстраполяции.
Например, динамика численности населения региона имеет следующую тенденцию (табл. 18).
Таблица 18
Динамика численности населения региона
| Показатель | 2000 г. | 2001 г. | 2002 г. | 2003 г. | 2004 г. | 2005 г. |
| Численность населения на 31 декабря, чел. | 54,5 | 55,8 | 57,5 | 59,1 | ||
| К роста (цеп.) | – | 1,02 | 1,03 | 1,025 | 1,03 | 1,028 |
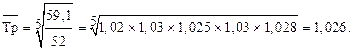
Если исходить из предположения, что данный темп роста сохранится на определенные промежутки и в дальнейшем или прошедшем, то можно определить численность, например, на 2022 г.:
у2022 = 59,1 × 1,02617 = 91,43 млн. чел.
или на 1999 г.:
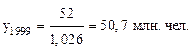
Аналогично производят и интерполяцию.
3. Прогнозирование на основе какой-либо аналитической формулы.Зная уравнение для исчисления теоретических уровней и подставляя в него значения t за пределами (внутри) исследуемого ряда, можно рассчитать для данных t вероятные значения уровней (yt).
Например, тенденция производства стали за 1985-1989 гг. характеризуется следующим образом:
yt = 120,8 + 5,21 × t,
t = –2 –1 0 1 2 3,
то для 2007 г.
y2007 = 120,8 + 5,21 × 17 = 209,37 млн. т,
y1986 = 120,8 + 5,21 × (–1) = –115,59 млн. т.
Дата добавления: 2014-12-23; просмотров: 396; Мы поможем в написании вашей работы!; Нарушение авторских прав |