Поступательное движение

Скорости всех точек в данный момент времени равны между собой и одинаково направлены (параллельны):

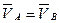
Плоскопараллельное движение. Это движение можно рассматривать как совокупность двух простейших движений – поступательного и вращательного (рис.4).

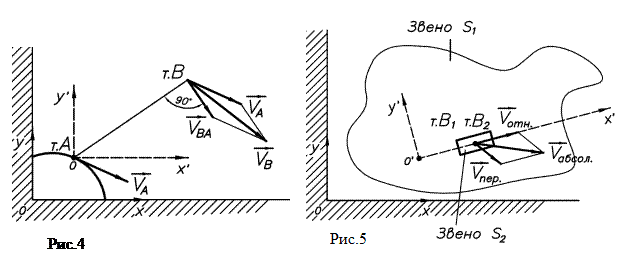
Скорость любой точки звена В, совершающего плоскопараллельное движение, представляет собой векторную сумму скорости полюса (скорость т.А) и скорости вращения точки вокруг полюса (т.В относительно т.А):

.

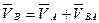За полюс всегда выбирается точка звена, скорость которой известна.

Сложное движение. Если точка совершает поступательное движение вокруг направляющей, которая в свою очередь, совершает вращательное или плоскопараллельное движение (рис.5), то такое движение точки называется сложным. Это движение характерно для кулисных механизмов.

Звено S₁, которому принадлежит т.В₁, совершает относительно неподвижной системы координат х-у (стойки механизма) в общем случае плоскопараллельное движение. Со звеном S₁ жестко связана система координат x’-y’. Вдоль направляющей О’x’ совершает поступательное движение звено S₂. Точка B₂ принадлежит звену S₂. Тогда движение, совершаемое т.B₁ относительно неподвижной системы отсчета x-y, называется переносным движением. Движение, совершаемое т.B₂ по отношению к подвижным осям x’-y’, называется относительным. Движение, совершаемое т.B₂ относительно неподвижной системы x-y, называется абсолютным.

На основании теоремы о сложении скоростей точки, совершающей сложное движение можно записать:

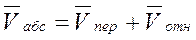
или

где 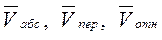– скорости абсолютного, переносного и относительного движений соответственно.

План скоростей и его свойства

План скоростей – построенный в определенном масштабе векторный график, характеризующий скорости всех точек и звеньев механизма. Произвольная точка , из которой производится построение плана скоростей, называется полюсом плана скоростей.

Построение плана скоростей основано на следующих его свойствах:

1. Неподвижные точки механизмы имеют соответствующие им точки плана скоростей, расположенные в полюсе.

2. Отрезки плана скоростей, проходящие через полюс, изображают абсолютные скорости. Векторы абсолютных скоростей направлены всегда от полюса.

3. Отрезки плана скоростей, не проходящие через полюс, определяют относительные скорости. Индекс относительной скорости содержит те же буквы, между которыми располагается вектор относительной скорости. Например, вектор 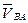, направлен от точки В к точке А.

4. Концы векторов абсолютных скоростей механизма, принадлежащих одному звену, образуют фигуры, подобные, сходственно расположенные и повернутые на 90° относительно фигур, образуемых этими точками на плане механизма.

Это свойство плана скоростей носит название теоремы подобия. Под сходственным расположением понимается следующее: если на плане механизма за точкой А по часовой стрелке следует т.В, а затем С, то и на плане скоростей в подобной фигуре по часовой стрелке за т.А должна следовать т.В, а затем т.С.

5. План скоростей позволяет определить величины и направления угловых скоростей.

При построении плана скоростей векторы скоростей точек откладываются с масштабным коэффициентом . Действительное значение скоростей получается путем умножения соответствующего отрезка плана скоростей на масштабный коэффициент скоростей.

Примеры построения плана скоростей