Пример 1. Построить план скоростей для кривошипно-шатунного механизма (рис.6а).

Построить план скоростей для кривошипно-шатунного механизма (рис.6а).

Дано: размеры звеньев, угловая скорость ведущего звена , положение ведущего звена .

Определить скорость точек А, В, С и угловую скорость звена 2.

1. Выбираем масштабный коэффициент плана положения механизма 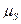и вычерчиваем методом засечек кинематическую схему механизма в заданном положении кривошипа.

2. Выбираем полюс плана скоростей .

3. Кривошип 1 совершает простое вращательное движение, при заданном положении кривошипа скорость точки А известна по величине –

и направлению – перпендикулярно звену АВ, в сторону вращения кривошипа (рис.6б).

Откладываем из полюса отрезок , изображающий скорость и определяем масштабный коэффициент скоростей:

4. Шатун 2 совершает плоскопараллельное движение, поэтому для точки В запишем уравнение:

Скорость т.А известна во величине и направлению (подчеркнем двумя чертами 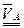). Скорость т.В относительно т.А известна только по направлению – перпендикулярна радиусу вращения (подчеркнем одной чертой и отметим, что ).

С другой стороны, т.В принадлежит ползуну 3, совершающему поступательное движение, поэтому направление движения т.В известно – вдоль направляющей . Подчеркиваем одной чертой и отмечаем, что .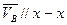

Графически решаем данное векторное уравнение: из конца вектора (точка a на плане скоростей) проводим прямую, перпендикулярную АВ, а из полюса проводим линию, параллельную . На пересечении этих линий ставим т.в. Отмечаем направление относительной скорости 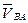, которая изображается вектором и абсолютной скорости (вектор на плане). Определяем их величины:

5. Для определения скорости т. С применим теорему подобия. На векторе плана скоростей построим треугольник подобный 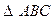, соблюдая правило обхода контура.

Для построения подобных треугольников ~ из т.а плана скоростей проводим прямую , а из т.в – прямую 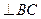. В пересечении этих линий получаем т.с, которая определяет конец вектора скорости т.С , начало которого находится в полюсе. Величина скорости т.С определяется:

6. Определяем угловую скорость шатуна 2 по формуле:

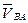Для определения направления перенесем вектор в т.В плана механизма. Как видно из чертежа, 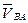создает вращение шатуна вокруг т.А по часовой стрелке. Угловая скорость направлена по часовой стрелке.