Основные положения. При построении плана ускорений используется следующие соотношения кинематики, определяющие ускорения в плоском движении.

При построении плана ускорений используется следующие соотношения кинематики, определяющие ускорения в плоском движении.

Вращательное движение. При вращении полное ускорение точки звена состоит из:

1. Нормального ускорения, направленного к центру вращения (рис.9) и равного:

где V_A – линейная скорость вращательного движения;

l_OA – радиус вращения.

2. Тангенциального ускорения, направленного перпендикулярно нормальному (рис.9), т.е. по скорости (при ускоренном) или против скорости (при замедленном) вращении, и равного:

где ε – угловое ускорение звена ОА.

Полное ускорение точки определяется векторной суммой:

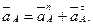
При равномерном вращении, когда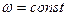

Поступательное движение. При поступательном движении ускорения всех точек звена равны между собой и параллельны друг другу.

Плоскопараллельное движение. Движение звена в этом случае может быть разложено на поступательное и вращательное, а ускорение точки В – на ускорение поступательного движения полюса ( 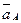) и ускорения вращательного движения точки относительно полюса ( ). Ускорение будет состоять из нормального , направленного к точке А, и тангенциального , перпендикулярного звену АВ. Ускорение точки можно записать в виде:

В данной векторной сумме ускорение 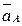известно, т.к. за полюс всегда выбирают точку, ускорение которой известно. Ускорение может быть определено по формуле:

где - угловая скорость звена АВ;

- длина звена АВ.

Ускорение определяется по формуле:

Сложное движение. Это движение (движение кулисных механизмов) раскладывается на переносное и относительное. Теорема сложения ускорений для точки, совершающей сложное движение, выглядит следующим образом:

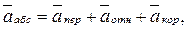
где – ускорение кулисы, которая совершает вращательное движение; может быть разложено на нормальное и тангенциальное:

(если ускорение точки кулисы известно, то раскладывать его на нормальное и тангенциальное не требуется).

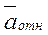– ускорение ползуна в относительном движении по кулисе (это движение поступательное и поэтому не раскладывается на составляющие);

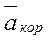– кориолисово ускорение.

Кориолисово ускорение представляет собой составляющую абсолютного ускорения точки в сложном движении и характеризует:

1. изменение модуля и направления относительной скорости точки вследствие относительного движения точки;

2. изменение направления относительной скорости вследствие вращательного переносного движения. Кориолисово ускорение определяется векторным произведением:

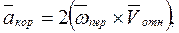
а величина , следовательно:

где α – угол между направлением относительной скорости и осью вращения переносного движения;

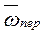– угловая скорость кулисы;

– относительная скорость ползуна, скользящего по кулисе.

В плоских механизмах угол α всегда равен 90^°, т.к. относительные скорости лежат в плоскости механизма, а оси вращения перпендикулярны этой плоскости. Кориолисово ускорение направлено перпендикулярно к вектору относительного ускорения. Направление кориолисова ускорения можно определить по правилу Н.Е. Жуковского. Графическая интерпретация этого правила состоит в следующем. Вектор относительной скорости закреплен в т. О (рис.10). Повернув вектор 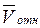на 90° в направлении (угловой скорости кулисы), получаем направление кориолисова ускорения.

План ускорений и его свойства

План ускорений – построенный в определенном масштабе векторный график, характеризующие ускорения всех точек и звеньев механизма. Произвольная точка р_а, из которой производится построение плана ускорений, называется полюсом плана ускорений.

Построение плана ускорений основано на следующих его свойствах:

1. Неподвижные точки механизмы имеют соответствующие им точки плана ускорений, расположенные в полюсе.

2. Отрезки плана ускорений, проходящие через полюс, изображают абсолютные ускорения. Векторы абсолютных ускорений направлены всегда от полюса.

3. Отрезки плана ускорений, соединяющие концы векторов абсолютных ускорений, изображают полные относительные ускорения.

4. Концы векторов абсолютных ускорений механизма, принадлежащих одному звену, образуют фигуры, подобные, сходственно расположенные и повернутые относительно фигур, образуемых этими точками на плане механизма.

Пользуясь теоремой подобия, подобную фигуру на плане ускорений необходимо строить методом засечек, соблюдая правило обхода контура.

5. План ускорений позволяет определить величины и направления угловых ускорений звеньев. Угловое ускорение звена направлено в сторону касательного ускорения.

При построении плана ускорений векторы скоростей точек откладываются в масштабе µ_а. Действительное значение ускорений получается путем умножения соответствующего отрезка плана ускорений на масштабный коэффициент плана ускорений.

Примеры построения плана ускорений