Пример 3

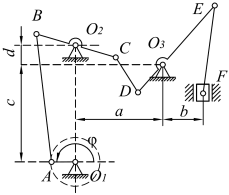
Построить план ускорений для кулисного механизма (рис.13).

Дано: размеры звеньев, угловая скорость ведущего звена , положение ведущего звена . Определить: ускорения точек механизма А, С, D, угловые ускорения звеньев 3, 4.

План механизма вычерчен в масштабе (рис.13а). Для механизма построен план скоростей (рис.13б).

1. Звено 1 вращается с постоянной угловой скоростью , поэтому:

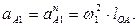
От полюса р_а параллельно ОА в направлении от т.А к т.О (рис.14б) откладываем вектор , изображающий ускорение т.А₁.

2. Как и при построении плана скоростей, движение т.А раскладываем на переносное (вращательное движение кулисы 3) и относительное (поступательное движение ползуна 2). Точка А₁ тождественна точке А₂ (А₁ = А₂), поэтому .

Движение шарнира А₂ рассматриваем как сложное: вместе с кулисой 3 и относительно кулисы 3. На основании описанной выше процедуры сложного движения запишем:

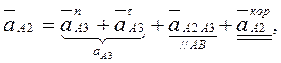
где - вектор абсолютного ускорения точки А₂, принадлежащей ползуну;

- вектор абсолютного ускорения т.А₃, принадлежащей кулисе. Кулиса совершает вращательное движение с угловой скоростью .

Величина ускорения определяется как:

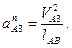
Направлено параллельно АВ от т.А к т.В; вектор направлен .

- вектор относительного ускорения т.А₂ относительно т.А₃ не известен по величине, но известен по направлению, параллелен АВ.

- кориолисово ускорение т.А₂:

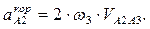
- определяется по плану скоростей.

- определяется по плану скоростей.

Направление определяется по правилу Жуковского (рис.14а) путем поворота вектора относительной скорости на 90° в направлении .

Решаем графически уравнение таким образом, чтобы известный вектор был замыкающим в многоугольнике ускорений. Для этого от полюса р в направлении от А к В параллельно АВ откладываем вектор , через конец которого проводим линию действия . Вектор - замыкающий, поэтому к другому его концу (т. а₂) пристраиваем известный вектор . Вектор можно пристраивать только так, как показано на плане ускорений (рис.14б). В противном случае вектор не будет замыкающим, т.е. результирующим векторной суммы.

Через начало вектора (т.а₂) параллельно АВ проводим линию действия относительного ускорения . В пересечении линий действия и получим точку а₃ – решение данного уравнения. Согласно правилу векторной суммы расставим направление векторов, как показано на рис. 12б.

Определяем значения ускорений:

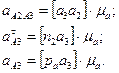
3. Определив ускорение т.А₃ и зная, что в полюсе плана ускорений расположена точка в, соответствующая ускорению неподвижного шарнира В, из пропорции находим положение т.с на плане ускорений: .

Вектор представляет собой абсолютное ускорение т.С механизма: .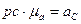

4. Для определения ускорения т. D составим уравнение:

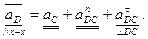
Абсолютное ускорение известно по направлению (// х–х), поэтому из полюса плана ускорений проводим прямую, параллельную х–х. К концу вектора параллельно DС в направлении от т.D к т.С пристраиваем вектор , величина которого .

Через конец вектора (т.d) проводим линию действия перпендикулярно DC. На пересечении этого перпендикуляра с горизонтальной прямой, проведенной через полюс р_а, представляющей линию действия , получим т.d – конец вектора 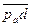, выражающего ускорение т.D.

Ускорения:

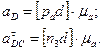
5. Величины и направления угловых ускорений звеньев определяем, как и в примере 1.

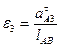- направлено против часовой стрелки.

- направлено по часовой стрелке.

ЗАДАНИЯ НА ПРАКТИЧЕСКУЮ РАБОТУ И ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ ОТЧЕТА

Требуется решить три основные задачи кинематического анализа механизма:

1. Построить план положения механизма в положении, заданном угловой координатой .

2. Построить план скоростей для всех подвижных точек механизма, указанных на схеме. Определить угловые скорости звеньев;

3. Построить план ускорений для указанных точек. Определить угловые ускорения звеньев.

Планы положения, скоростей и ускорений построить на листе формата А3 с обязательным указанием масштабных коэффициентов. Номер варианта выдается преподавателем.

Структурные схемы и размеры звеньев приводятся в таблицах 2 – 4.

Задания I типа (№ 1 – 30) [2] рекомендуются для студентов, изучающих теорию механизмов и машин в курсах «Прикладная механика», «Теоретическая механика», «Механика». Для их выполнения достаточно рассмотреть примеры 1 и 2.

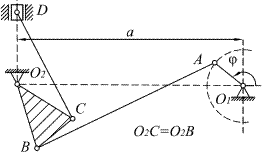
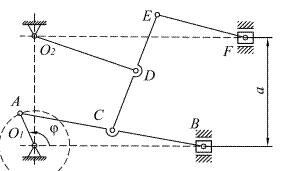
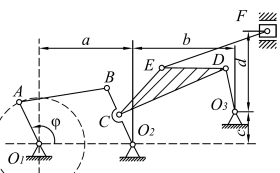
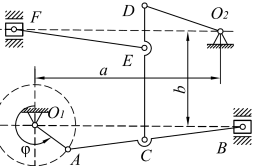
Задания II типа (№ 31 – 50) (кулисные механизмы) выполняются после рассмотрения примеров 1, 2 и 3.

Таблица 2. Числовые данные заданий I типа

№ варианта	φ, град.	Длина звеньев, м	Расстояния, м
		0,18	0,23	0,18	0,22	0,23	0,14	0,28	-	0,28	-	0,21	0,21	0,48	0,38	-	0,42
		0,56	0,10	0,26	0,16	0,25	0,21	0,25	-	-	0,20	0,54	0,52	0,69	0,35	-	0,32
		0,15	0,25	0,54	0,35	-	0,15	0,28	-	0,58	-	0,42	0,21	0,47	0,26	-	0,31
		0,26	0,15	0,23	-	-	0,15	0,65	-	-	-	0,51	0,22	0,38	-	-	-
		0,19	0,19	0,10	0,22	-	0,12	-	0,19	-	-	0,55	0,19	0,23	-	0,38	0,22
6		0,65	0,49	-	-	-	0,15	0,29	-	0,24	-	0,50	0,25	0,32	0,23	-	0,39
		0,11	0,42	0,11	0,07	0,24	0,16	0,34	-	-	0,41	0,25	0,25	0,42	0,21	-	0,49
		0,27	0,18	0,14	0,15	0,30	0,14	0,29	-	0,23	-	0,55	0,32	0,15	-	0,45	-
		0,23	0,19	0,20	0,28	0,21	0,21	0,31	-	0,25	-	0,65	0,62	0,31	-	0,11	0,29
		0,55	0,21	0,25	-	-	0,15	-	0,24	-	-	0,70	0,35	0,33	-	0,17	0,12
		0,50	0,30	-	-	-	0,14	0,29	-	-	-	0,45	0,54	0,34	-	0,37	-
		0,10	0,86	0,32	0,28	-	0,21	-	-	0,55	-	0,60	0,30	0,19	0,60	-	0,49
		0,17	0,54	-	-	-	0,15	-	0,40	-	-	0,50	0,35	0,40	0,22	0,22	0,50
		0,28	0,40	0,06	0,18	0,15	0,15	0,31	-	0,15	-	0,50	0,25	0,70	0,35	-	0,50
		0,46	0,31	-	-	-	0,15	0,20	-	0,20	-	0,45	0,15	0,31	0,17	0,17	0,37
		0,36	0,22	0,15	-	-	0,15	0,20	0,40	-	-	0,45	0,20	0,24	-	0,40	-
		0,96	-	-	-	-	0,15	0,28	-	-	-	0,84	0,20	0,51	-	-	-
		0,70	0,09	0,37	-	-	0,16	-	0,39	-	0,25	0,78	0,38	0,41	0,19	-	0,57
		0,42	0,39	-	-	-	0,20	-	0,20	-	-	0,71	0,30	-	-	0,57	-
		0,27	0,24	0,30	-	-	0,20	0,50	-	-	0,30	0,80	0,32	0,58	0,29	-	0,35
		0,46	-	-	-	-	0,15	-	0,45	-	-	0,78	0,39	0,26	0,52	-	0,38
		0,46	0,23	0,11	-	-	0,15	0,15	-	0,38	-	0,44	0,25	0,30	0,22	0,15	0,40
23		0,31	0,30	0,50	-	-	0,15	0,30	-	0,50	-	0,40	0,16	0,60	0,30	-	0,30
		0,36	0,39	0,13	0,31	-	0,17	0,23	-	0,17	-	0,35	0,11	0,45	0,25	0,25	0,44
		0,72	0,36	-	-	-	0,15	-	0,30	-	-	0,76	0,46	0,50	0,35	-	0,51
		0,36	0,53	0,36	0,32	-	0,19	0,40	-	-	0,19	0,76	0,38	0,68	0,35	-	0,29
		0,71	0,27	0,32	0,40	-	0,16	0,30	-	0,50	-	0,46	0,33	0,40	0,20	-	0,50
		0,30	0,20	0,35	-	-	0,19	-	0,19	-	-	0,59	0,29	0,24	-	0,48	0,36
		0,35	0,15	0,38	0,07	-	0,10	0,16	-	0,15	-	0,50	0,33	0,16	-	0,45	0,33
30
	0,46	0,28	0,17	-	-	0,16	0,25	-	0,75	-	0,50	0,11	0,33	-	0,26	0,44

Таблица 2 Задания I типа
1.	2.
5. 3.	4. 6.
7.	8.
11. 9.	12. 10.
13.	14.
15.	16.
17.	18.
19.	20.
21.	22.
23.	24.
25.	26.
27.	28.
29.	30.
Задания II типа
31.	32.
33.	34.
35. 37.	36. 38.
39.	40.

СПИСОК ЛИТЕРАТУРЫ

1. Прикладная механика: учебник для вузов/ В.В. Джамай, Ю.Н. Дрозов, Е.А. Самойлов и др.; под ред. В.В. Джамая. – М.: Дрофа, 2004. – 414 с

2. Сборник заданий для курсовых работ по теоретической механике. Учебное пособие для вузов/ Под ред. А.А. Яблонского. – 15-е изд., стер. – М.: Интеграл – Пресс, 2006 – 384 с

3. Хлебосолов О.Г. Графоаналитические методы расчета механизмов с использованием ЭВМ// Теория механизмов и машин. – 2004, №2 (4),с. 40 – 44