Порядок виконання завдання. M1-я= , M2-я= . Далі слід розрахувати середнє значення кожної змінної в окремих групах для визначення положення центрі

1. Необхідно представити дані у вигляді матриць M1 и M2:

M_1-я= , M_2-я= .

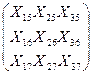1. Далі слід розрахувати середнє значення кожної змінної в окремих групах для визначення положення центрів цих груп.
2. На наступному етапі розраховуються коефіцієнти для дискримінантної функції:

(5.36)

Коефіцієнти а₁, а₂ и а₃ розраховуються за формулою 6.1:

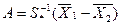(5.37)

де - вектори середніх в першій і другій групах;

А - вектор коефіцієнтів;

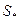^-1 - матриця, зворотна спільній ковариационной матриці.

Для визначення спільної ковариационной матриці S* потрібно розрахувати матриці S₁ і S₂. Кожен елемент цих матриць є різницею між відповідним значенням вихідної змінної х_ij і середнім значенням цієї змінної в даній групі 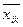(k - номер групи):

;

де 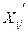- транспонована матриця відхилень спостережуваних значень вихідних змінних від їх середніх величин.

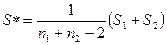, (5.38)

где n₁, n₂ – число об’єктів 1-ої и 2-ої груп.

4. Далі по формулі 6.2 розраховуємо вектор коефіцієнтів функції дискримінанта.

5. Підставляємо набутих значень коефіцієнтів у формулу 5.36 і розраховуємо значення функції дискримінанта для кожного об'єкту і знаходимо середні значення.

6. На наступному етапі виробляється розрахунок константи дискримінації С по формулі 5.39:

С=1/2( 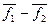) (5.39)

Після здобуття константи дискримінації можна перевірити правильність розподілу об'єктів у вже існуючих двох класах, а також провести класифікацію нових об'єктів. Для того, щоб віднести об'єкти до одного з двох безлічі, необхідно розрахувати для них значення функцій дискримінантів (по трьох змінним).

Практичне заняття 6