
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Потери мощности и энергии в тяговой сети
Промышленность выпускает трансформаторы различных типов, причем, каждый тип – на ряд номинальных мощностей. Любой из этих трансформаторов может передавать мощность, большую и меньшую номинальной. В первом случае, в нем увеличивается потери мощности и, соответственно, температура обмотки, во втором, уменьшаются потери мощности и температура обмотки.
Увеличение температуры обмотки вызывает необратимые процессы в материале ее изоляции, которые называют старением, или износом изоляции. При этом срок службы трансформатора уменьшается. Кроме того, резкое увеличение нагрузки может привести к опасному повышению температуры масла в верхних слоях до близкой к температуре его вспышки. Согласно стандарту на нагрузочную способность силовых трансформаторов и автотрансформаторов наибольшая температура масла в верхних слоях и в наиболее нагретой точке обмотки в течение переходного суточного процесса нагрева не должна превосходить соответственно 95 и 140 0С.
Можно считать, что мощность трансформатора выбрана правильно, если срок службы будет не менее нормативного и по возможности наиболее близким к нему. Но рассчитать срок службы трансформатора или износ при заданной нагрузке можно, только зная его номинальную мощность.
Температура обмотки трансформатора зависит от значения потерь энергии в ней, обращающихся в тепло. Но потери мощности во времени претерпевают большие изменения, вследствие колебания нагрузки в подстанционной зоне. Поэтому при одних и тех потерях энергии температура может изменяться в широких пределах. Так как повышение ее ведет к резкому непропорциональному ускорению старения изоляции, то наименьшее старение, а следовательно, наименьшая мощность трансформаторов понадобилась бы в условиях, когда фактически выделяемое тепло в обмотках трансформатора распределялось бы равномерно в течение пропорционально квадрату тока, то оно, а следовательно, и мощность трансформатора соответствовали бы среднему квадратичному току нагрузки подстанции  . Следовательно, минимальная мощность, выше которой должна быть требуемая мощность трансформатора, может быть определена по формуле:
. Следовательно, минимальная мощность, выше которой должна быть требуемая мощность трансформатора, может быть определена по формуле:
 (3.19)
(3.19)
Согласно ГОСТ 14209-85 относительный износ следует определять по формуле:
 ; (3.20)
; (3.20)
где  - температура наиболее нагретой точки обмотки в 0С;
- температура наиболее нагретой точки обмотки в 0С;  - базовая температура наиболее нагретой точки обмотки, при которой скорость расчетного износа витковой изоляции соответствует сроку службы трансформатора, условно принятому за единицу,
- базовая температура наиболее нагретой точки обмотки, при которой скорость расчетного износа витковой изоляции соответствует сроку службы трансформатора, условно принятому за единицу,  .
.
Из этой формулы непосредственно вытекает так называемое шестиградусное правило, которое заключается в том, что каждое изменение температуры обмотки на 6 0С ведет к изменению в два срока службы трансформатора (уменьшению при увеличении температуры и увеличению при ее уменьшении).
После определения отношений по формуле (3.18) следует найти среднюю интенсивность износа изоляции обмотки трансформатора в сутки предоставления окна:
 , (3.21)
, (3.21)
где,
 . (3.22)
. (3.22)
Здесь  - температура окружающей среды в период восстановления нормального движения, задается от района в исходных данных.
- температура окружающей среды в период восстановления нормального движения, задается от района в исходных данных.
 (3.23)
(3.23)
 (3.24)
(3.24)
 . (3.25)
. (3.25)
В формулах (3.23 - 3.25) a, b, g, h – постоянные в выражениях, аппроксимирующие зависимости разности температур обмотка – масло и масло – окружающая среда (они равны: а=17,7; b=5,3; g=39,7; h=15,3  );
);  - тепловая постоянная времени масла, 3 часа;
- тепловая постоянная времени масла, 3 часа;  - среднее время хода поезда по фидерной зоне.
- среднее время хода поезда по фидерной зоне.
Пример расчета:
 мин.
мин.
переводим в часы 45,83/60=0,76384 ч.

 ;
;
 ;
;
 ;
;
 .
.
Если  , то по полученной интенсивности износа F1 производится пересчет номинального тока. Находится такой расчетный номинальный ток, при котором относительная интенсивность износа будет нормальной, по формуле:
, то по полученной интенсивности износа F1 производится пересчет номинального тока. Находится такой расчетный номинальный ток, при котором относительная интенсивность износа будет нормальной, по формуле:
 (3.26)
(3.26)
где  — число суток с предоставлением окон в год, в курсовом проекте можно принять равным 2/3 числа суток в весенне-летний период.
— число суток с предоставлением окон в год, в курсовом проекте можно принять равным 2/3 числа суток в весенне-летний период.
Пример расчета:
В нашем случае  , то производим пересчет номинального тока:
, то производим пересчет номинального тока:

 сут.
сут.
 - коэффициент использования пропускной способности равен:
- коэффициент использования пропускной способности равен:
 .
.
Как показали специально выполненные исследования, выбор мощности трансформатора по току  (в предположении, что износ изоляции обмотки происходит только в период восстановления нормального движения после окна) может привести; к ее занижению не более, чем па 8%.
(в предположении, что износ изоляции обмотки происходит только в период восстановления нормального движения после окна) может привести; к ее занижению не более, чем па 8%.
Поэтому необходимая расчетная мощность может лежать в пределах  и
и  , равных:
, равных:

 (3.27)
(3.27)
В случае, когда по этим формулам получается, что
 или
или  ,
,
то надо принять:
 .
.
 .
.
Если по стандартной шкале мощность трансформаторов, выбранная по  и
и  , будет одна и та же, то на этом выбор трансформатора по износу заканчивается.
, будет одна и та же, то на этом выбор трансформатора по износу заканчивается.
В тех редких случаях, когда стандартная мощность трансформаторов, выбранная по  и
и  , будет различной, надо провести уточненный расчет.
, будет различной, надо провести уточненный расчет.
Пример расчета:
 кВА;
кВА;
 кВА.
кВА.
Выбираем два трансформатора по 40 МВА. Выбранные по износу изоляции трансформаторы проверяем по максимально допустимому току и максимально допустимым температурам обмотки масла.
Обозначим выбранную по каталогу, исходя из интенсивности износа изоляции, мощность трансформаторов через  . Тогда ток, соответствующий располагаемой мощности для тяги, найдем из
. Тогда ток, соответствующий располагаемой мощности для тяги, найдем из
 ; (3.28)
; (3.28)
Если по формуле (3.23) получится  , то
, то  надо приравнять
надо приравнять  .
.
 .
.
Краткость нагрузки при выбранной мощности трансформатора  определяется для суток с предоставлением окна.
определяется для суток с предоставлением окна.
Расчет для таких суток базируется на замене реального графика эквивалентным двухступенчатым ([2], рисунок 8.10)
Нетрудно показать, что для условий проекта

При таком соотношении, согласно упомянутому приложению, следует принимать

 ;
;
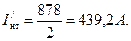
Максимальная температура масла может быть определена по формуле:
 (3.29)
(3.29)
а обмотки по:
 . (3.30)
. (3.30)
Если окажется, что  °С или
°С или  °С, то надо принять следующий по мощности трансформатор.
°С, то надо принять следующий по мощности трансформатор.
Значения входящих в формулы (3.29) и (3.30) токов  так же как и коэффициента
так же как и коэффициента  , были найдены ранее.
, были найдены ранее.
На тяговых подстанциях переменного тока обычно устанавливают два трансформатора одинаковой мощности. Учитывая это и зная общую трансформаторную мощность, можно выбрать номинальную мощность одного трансформатора  . При этом можно ориентироваться на следующие номинальные мощности трансформаторов: 16; 25; 40 и 63 МВ·А.
. При этом можно ориентироваться на следующие номинальные мощности трансформаторов: 16; 25; 40 и 63 МВ·А.
В нормальных условиях заданные размеры движения должны быть обеспечены при работе одного трансформатора. Это возможно, если:
 (3.31)
(3.31)
 (3.32)
(3.32)
где  — ток, соответствующий мощности, которая может быть использована для тяги при работе одного трансформатора. Он определяется по формуле (3.16) с учетом следующих за ней пояснений при работе одного трансформатора.
— ток, соответствующий мощности, которая может быть использована для тяги при работе одного трансформатора. Он определяется по формуле (3.16) с учетом следующих за ней пояснений при работе одного трансформатора.
Пример расчета:
 а обмотки по:
а обмотки по:

Как уже отмечалось ранее, что, если окажется, что  или
или  , то надо принять следующий по мощности трансформатор, в нашем случае:
, то надо принять следующий по мощности трансформатор, в нашем случае:  ,
,  .
.
Значит, оставляем выбранные трансформаторы.


 (по условию должно быть меньше 950С)
(по условию должно быть меньше 950С)
 (по условию должно быть меньше 1400С)
(по условию должно быть меньше 1400С)
Т.к. условия не выполняются, трансформатор не может обеспечить заданные размеры движения. Окончательно принимаем следующий по номенклатурной мощности трансформатор.
При этом можно ориентироваться на следующие номинальные мощности трансформаторов:16; 25; 40 и 63 МВА.
В нормальных условиях заданные размеры движения должны быть обеспечены при работе одного трансформатора, в нашем случае выбираем:
ТДТНЭ – 63 000/110 (два трансформатора)
Полная мощность тяговой подстанции:

Выбор сечения проводов контактной сети следует произвести для одной фидерной зоны двустороннего питания. Для определения экономического сечения проводов контактной сети можно использовать метод, изложенный в [2].
При протекании тока по проводам часть энергии рассеивается и для потребителя является потерянной, поэтому она и получила название «потерь энергии». Количество этой энергии находится в непосредственной зависимости от площади поперечного сечения и материала проводов, а при переменном токе – и от взаимного расположения их. С увеличением сечения проводов уменьшается потеря энергии. Но увеличиваются капитальные затраты на сеть. Необходимо определить оптимальное сечение проводов, при котором приведенные ежегодные расходы будут наименьшими.
В этом случае, общее сечение проводов контактной сети в медном эквиваленте будет равно:
 , (3.33)
, (3.33)
где Кэ - стоимость электрической энергии, тг./кВт·ч; Во - годовые удельные потери в проводах контактной сети рассматриваемой фидерной зоны; кВт·ч/Ом·год.
Для условий курсового проекта примем Кэ = 15,8 тг/кВт·ч (приложение 5).
Тогда экономическое сечение можно определить по формуле:
 . (3.34)
. (3.34)
Для определения Во следует воспользоваться формулами для расчета энергии потерь в проводах контактной сети.
При раздельной работе путей Во и Fм определяются для каждого пути отдельно.
Суточный расход энергии, являющийся одной из исходных данных величин расчета, легко определяется по подсчитанным ранее средним токам поездов, времени их хода по фидерным зонам, напряжению, которое принято для тяговых расчетов 25 кВ, и заданному количеству поездов за сутки.
Расчетными размерами движения при определении экономического сечения и энергии потерь будут средние за год суточные размеры движения. Так как в приложении 4 указаны размеры движения в сутки наибольшей интенсивности движения, то при определении Во надо разделить их на коэффициент неравномерности  .
.
Таким образом,
 , (3.35)
, (3.35)
где  - средний ток поезда;
- средний ток поезда; 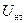 =25 кВ – напряжение в контактной сети;
=25 кВ – напряжение в контактной сети;  - время хода поезда по фидерной зоне;
- время хода поезда по фидерной зоне;  - расчетное число поездов,
- расчетное число поездов,  ,
,  =1,15 - коэффициент неравномерности движения поездов.
=1,15 - коэффициент неравномерности движения поездов.
Пример расчета:
 ;
;
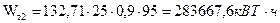 .
.

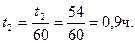
Энергию потерь за время Т в этом случае для каждого пути можно найти без учета влияния соседнего пути по формуле [2]
 . (3.36)
. (3.36)
где 
 - активное сопротивление одного километра контактной сети одного пути, Ом/км;
- активное сопротивление одного километра контактной сети одного пути, Ом/км;  - длина фидерной зоны, км;
- длина фидерной зоны, км;  - напряжение контактной сети, кВ (
- напряжение контактной сети, кВ (  );
);  - расход энергии на движение поездов по фидерной зоне за период Т;
- расход энергии на движение поездов по фидерной зоне за период Т;  - суммарное время потребления энергии всеми
- суммарное время потребления энергии всеми  поездами, проходящими за период Т фидерную зону;
поездами, проходящими за период Т фидерную зону;  - суммарное время занятия всеми расчетными поездами фидерной зоны за период Т., значение Тпер делим на 60 мин. Остальные обозначения те же, что и ранее.
- суммарное время занятия всеми расчетными поездами фидерной зоны за период Т., значение Тпер делим на 60 мин. Остальные обозначения те же, что и ранее.
Годовые потери составят  , а удельные потери
, а удельные потери  .
.
Пример расчета:


где 


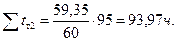
Подставляя  из (3.36) при однотипных поездах, получим
из (3.36) при однотипных поездах, получим
 . (3.37)
. (3.37)
Принимая в этой формуле  для первого пути (
для первого пути (  .) найдем
.) найдем  -удельные потери для этого пути. Таким же образом, но по расходу энергии на движение поездов по фидерной зоне второго пути определим удельные потери на втором пути
-удельные потери для этого пути. Таким же образом, но по расходу энергии на движение поездов по фидерной зоне второго пути определим удельные потери на втором пути  .
.
После этого, по формуле (3.34) нетрудно найти экономические сечения проводов и выбрать несущий трос.
Пример расчета:




При узловой схеме (рисунок 3.3)

Рисунок 3.3 Узловая схема контактной сети
общий расход энергии на движение поездов по обоим путям рассматриваемой фидерной зоны за расчетный период будет равна:
 ; (3.38)
; (3.38)
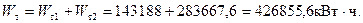
При узловой схеме (рисунок 3.3) выражение для энергии потерь в проводах контактной сети имеет вид:
 ; (3.39)
; (3.39)
где  и
и  - время потребления энергии при проходе фидерной зоны соответственно поездами нечетного и четного направлений;
- время потребления энергии при проходе фидерной зоны соответственно поездами нечетного и четного направлений;  и
и  - общее время хода по фидерной зоне поездов нечетного и четного направлений,
- общее время хода по фидерной зоне поездов нечетного и четного направлений,  - активное сопротивление контактных подвесок обоих путей.
- активное сопротивление контактных подвесок обоих путей.
Откуда получим выражение для Во при узловой схеме
 ;(3.40)
;(3.40)
В формулы (3.32) и (3.35) входят члены  и
и  - соответственно. Они должны учитываться только при положительном их значении. Если они при расчете получатся отрицательными, то их надо отбросить (приравнять нулю).
- соответственно. Они должны учитываться только при положительном их значении. Если они при расчете получатся отрицательными, то их надо отбросить (приравнять нулю).
В соответствии с изложенным ранее все величины, входящие в формулы, должны быть отнесены к расчетному периоду Т=24 ч.
Пример расчета:
 ;
;


Годовые потери составят:
 ;
;
Далее по формуле (3.34) найдем суммарное сечение проводов контактной сети на два пути. На один путь сечение будет в два раза меньше.
При раздельной схеме питания рассчитываем экономическое сечение проводов для обоих путей:
- четный путь

-нечетный путь

Производим выбор контактной подвески по допустимому сечению
 ;
;  .
.
Принимаем контактную подвеску:
 ;
;  .
.
После выбора сечения проводов контактной сети можно найти для нее абсолютное значение энергии потерь. Это легко сделать, используя ранее определенную величину Во,
 (3.41)
(3.41)
Активное сопротивление в контактной сети дается в таблице 3.1 [2,3].
Таблица 3.1
Активные сопротивления контактной подвески
| Типы подвески | ПБСМ70 + + МФ100 | ПБСМ95 + +МФ100 | М95 + + МФ100 | М120 + + МФ100 | |
| r, Ом/км | Без усил. провода | 0,166 | 0,151 | 0,092 | 0,082 |
| С усил. проводом А185 | 0,089 | 0,083 | 0,059 | 0,055 |
Энергию потерь в рельсах можно не находить, так как она одинакова для обеих схем и, следовательно, не отразится на результатах их экономического сравнения.
После выбора экономического сечения необходимо проверить его по нагреванию (п.4 задания)
 , (3.42)
, (3.42)
где  - допустимый ток выбранной контактной подвески
- допустимый ток выбранной контактной подвески  ;
;  - максимальный эффективный ток для данной фидерной зоны по расчету.
- максимальный эффективный ток для данной фидерной зоны по расчету.
Студент должен выбрать и обосновать метод этой проверки. В частности, может быть использован (при обосновании) способ проверки контактной подвески по эффективному току, который надо сравнить с допустимым для выбранной подвески.
В этом случае можно использовать ранее найденные по формуле (3.11) значения токов фидеров, заменив заданное число поездов N на число поездов при полном использовании пропускной способности N0.
Дата добавления: 2014-12-23; просмотров: 352; Мы поможем в написании вашей работы!; Нарушение авторских прав |