
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Средние и эффективные токи подстанции
После определения средних нагрузок фидеров подстанции могут быть найдены линейные нагрузки (нагрузки плеч, рисунок 3.2).
Для двухпутного участка будем иметь средние токи плеч:
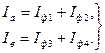 , (3.12)
, (3.12)
и квадраты эффективных токов плеч:
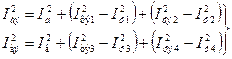 . (3.13)
. (3.13)
Из формул (3.4), (3.5) видно, что фидерные токи зависят от коэффициента использования пропускной способности 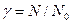 . Его следует брать каждый раз соответствующим расчетному режиму.
. Его следует брать каждый раз соответствующим расчетному режиму.
Пример расчета:
Используя вышеуказанные формулы (3.12, 3.13), произведем соответствующие расчеты:

где  ,
,  ,
,  ,
,  - значения рассчитанные по формуле (3.9)
- значения рассчитанные по формуле (3.9)
Квадраты эффективных токов плеч:
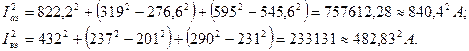
Из-за большой постоянной времени нагревания масла было бы неправильно определять повышение температуры масла над температурой окружающей среды, исходя из максимально возможной нагрузки, так как она не может поддерживаться в течение длительного времени. Но наибольшая разность температур обмотки и масла практически будет наибольшей при максимальной нагрузке, так как тепловая постоянная времени обмотки мала.
Нагрев масла в трехфазном трансформаторе будет определяться потерями в обмотках трех фаз, которые при несимметричной нагрузке будут неодинаковы.
Для учета этого можно оперировать эквивалентным эффективным током фазы, который вызовет при симметричной нагрузке те же потери, что и действительные несимметричные нагрузки.
Из сказанного ранее следует, что такой эквивалентный ток должен быть найден не только для условии нормального графика движения, но и для периода восстановления нормального движения после окна при  . Кроме того, для проверки температуры обмотки должен быть найден эффективный ток обмотки при максимальных размерах движения. Этот ток может быть найден по формулам, приведенным в учебнике [2] при приравнивании размеров движения N пропускной способности N0. За расчетный берется ток той обмотки, для которой он имеет наибольшее значение.
. Кроме того, для проверки температуры обмотки должен быть найден эффективный ток обмотки при максимальных размерах движения. Этот ток может быть найден по формулам, приведенным в учебнике [2] при приравнивании размеров движения N пропускной способности N0. За расчетный берется ток той обмотки, для которой он имеет наибольшее значение.
Ниже приводится формула для расчета тока обмоток «а» и «с» в предположении, что углы сдвига фаз средних нагрузок на обоих плечах равны:
 (3.14)
(3.14)
Для определения максимального эффективного тока обмотки  значения величин
значения величин  ,
,  ,
,  и
и 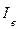 должны быть рассчитаны, как указывалось, при
должны быть рассчитаны, как указывалось, при  . За ток
. За ток  принимается больший из токов
принимается больший из токов  или
или  .
.
Эквивалентные по нагреву масла токи обмотки при том же предположении могут быть найдены по формуле [2, с. 410]:
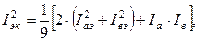 (3.15)
(3.15)
 .
.
По этой же формуле находят эквивалентный по нагреву масла ток обмотки при заданных размерах движения 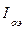 , подставляя в нее
, подставляя в нее  ,
,  ,
,  ,
, 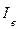 рассчитанные для этих размеров движения, и ток
рассчитанные для этих размеров движения, и ток  в период восстановления нормального графика после окна. В этом случае
в период восстановления нормального графика после окна. В этом случае  ,
,  ,
,  ,
, 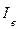 определяются для увеличенных в отношении 0,9
определяются для увеличенных в отношении 0,9  размеров движения.
размеров движения.
Пример расчета:
Режим максимального размера движения (приравниваем 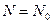 ):
):
Средние токи фидеров:
 ;
;
 ;
;
 ;
;
 ,
,
где  ,
,  ,
,  ,
,  - значения, рассчитанные по формуле (4.4)
- значения, рассчитанные по формуле (4.4)
Квадраты эффективных токов фидеров  :
:
 ;
;
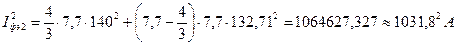 ;
;
 ;
;
 .
.
Средние токи плеч:

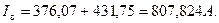
Эффективные токи плеч:

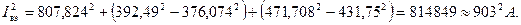
Для определения максимального эффективного тока обмотки 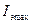 , рассчитываем токи обмоток «a» и «с» в предположении, что углы сдвига фаз средних нагрузок на обоих плечах равны:
, рассчитываем токи обмоток «a» и «с» в предположении, что углы сдвига фаз средних нагрузок на обоих плечах равны:
 ;
;
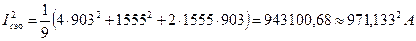 .
.
За 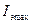 принимаем наибольший из токов
принимаем наибольший из токов  или
или  :
: 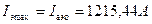 .
.
Дата добавления: 2014-12-23; просмотров: 512; Мы поможем в написании вашей работы!; Нарушение авторских прав |